Editorial Board
Graduate Students
- Lin Chen
- Ruiyu Han
- Sangmin Park
Postdocs
- Lihan Wang
Former Graduate Students
- Jeff Eisenbeis (PhD 2017, HERE Technologies)
- Nicolas Garcia Trillos (PhD 2015, Prager Assistant Professor, Brown University)
- Slav Kirov (PhD 2017, Eigen Technologies)
- Robert Simione, (PhD 2014, Canvs).
- Andrew Warren, (PhD 2022, Institut des Hautes Études Scientifiques (IHES))
- Lantian Xu (PhD 2024, Tower Research Capital)
- Lijiang Wu (PhD 2015, Goldman Sachs)
- Danlei Zhu (PhD 2023, Akuna Capital)
Former Postdocs
- Xin Yang Lu (postdoc at McGill)
- Francesco Patacchini (IFP Energies nouvelles)
- Matthew Thorpe (postdoc at Cambridge)
I am interested in using techniques of applied analysis, calculus of variations, and PDE in analyzing the data clouds, graph-based representations of data, and datasets of images. Here are a few ongoing projects:
Together with Nicolas Garcia Trillos, I have been studying properties of perimeter on random geometric graphs. Such graphs arise when one considers data cloud, V, obtained by sampling some distribution (say supported on a manifold, with continuous density). The weighted graph representing the configuration is obtained by giving weights to edges between points based on the distances. This includes setting a length scale,
ε, such that significant weight is given to edges of length up to ε. The perimeter of A ⊂ V is defined based on weights of edges between A and
V \A. Perimeter arrises naturally in a variety of objective functionals related to data analysis tasks such as clustering and classification. It is of interest to know
if, when large number of data points is available, this perimeter behaves like the continuum perimeter on the underlying distribution. In particular if the minimizers of functionals on graphs involving the graph perimeter will be close to minimizers of the continuum functional. For that reason we investigate a variational notion of convergence known as the Γ-convergence.
We investigate under which scaling of ε on N do does the graph perimeter Γ-converge to the perimeter in the Euclidean space.
Together with Xavier Bresson and Thomas Laurent, Nicolas and I are considering applications to particular functionals, like the balanced cut, and investigating numerically how small neighborhoods (i.e. how small ε) can be taken.
In 2009, Gustavo Rohde and I started investigating the use of optimal transportation distances as a measure of similarity between images. The collaboration has since involved Saurav Basu, C. Chen, Soheil Kolouri, Ann Lee, Di Liu, John Ozolek, and Wei Wang. The basic observation is that for certain classes of images, in particular ones which represent a measurement of some quantity that has a relatively irregular distribution and has few geometric constraints, optimal transportation and related distances are a natural tool to measure similarity. Such classes of images are abundant in biology and we applied our techniques to images of chromatin in nuclei and proteins in cells. We introduced a distance related to optimal transportation, which we call the linear optimal transportation, which preserves many desirable features of optimal transportation, but is much faster to compute. Our approach also facilitates many of the statistical tasks as it provides an isometric embedding into a Euclidean space. We are continuing to work on devising distances which measure the relevant differences between images (in 2D and 3D) and building a computational framework for their use. The distances of our interest are deformation based, and provide a geometric description of the space of images.
Approximating and representing a point cloud using a simpler and lower dimensional object can be formulated as a variational problem. Namely one defines an objective functional which penalizes the approximation error and the complexity of the answer. With Slav Kirov and Xin-Yang Lu, I have considered using one-dimensional objects, namely curves and trees, to approximate data. We found a connection between the average-distance problem (which is a mathematical problem introduced in network planning) and (regularized) principal curves considered in statistics and machine learning. We discovered that despite of the presence of the regularizing term the minimizer of the problem can be a Lipschitz curve with corners. Nevertheless the total curvature (considered as a measure) can be controlled. Xin-Yang and I proved a sharp a priory estimate on the total curvature in terms of the total amount of data and the parameters of the functional This gives insight on how exactly can the parameters be used to tune the complexity of the answer. As above it is of interest to consider what happens with the minimizers if more and more data sampled out of a fixed distribution are given. We show that as the number of data points goes to infinity the topology of the minimizer cannot keep getting more complicated, that is a topological lower-semicontinuity of minimizers holds. The fact that the minimizers may have corners is undesirable from the data-analysis standpoint sing a nonnegligible fraction of data projects to a single point leading to a loss of information. We are working on modifying the functionals to eliminate this problem. With Slav Kirov we are working on an efficient and robust numerical implementation of the optimization problems.
Nonlocal interaction equations arise in models of biological aggregation, and many systems where there is a pairwise interaction between particles/individuals/agents at a distance, such that the resulting particle velocities are proportional to the "force". Such systems exhibit a surprisingly reach behavior which can be quite sensitive to the details of the interaction between particles. The models can often be formulated in the framework of gradient flows in spaces of probability measures which allows for unified treatment of the particle and continuum descriptions. In studying these systems I collaborated with Andrea Bertozzi, Jose Antonio Carrillo, Marco Di Francesco, Jeff Eisenbeis, Alessio Figalli, Thomas Laurent, Bob Pego, Robert Simione, and Lijiang Wu. Here are some of the ongoing projects by/with my graduate students:
Jeff Eisenbeis has introduced a new model for biological aggregation in which the response of individuals to stimuli depends on the whole configuration. In particular it takes into account that the influence of individual an B on an individual A depends on whether there are other individuals near A. In particular its influence will be diminished if A there are other individuals near A. What is surprising about this model is that it still has a gradient flow structure as the original model. Namely if one considers a nonlocal mobility then the system becomes a gradient flow of a modified potential with respect to geometry of the configuration space provided by the nonlocal mobility. In the standard case, with local mobility, the geometry of the configuration space is the Wasserstein metric. The nonlocal mobility provides a new and interesting geometry which leads to new effects. Some of these are what one would indeed expect from a group of individuals moving in a way that takes into account that moving is more difficult in crowded places.
This is work with Robert Simione. It has been observed that depending on the potential the nonlocal-interaction equations can have a steady states of large variety of shapes and properties, including those supported on finite sets, on rings, on sets of full dimension, both radially symmetric and without symmetry. This holds even if one only considers smooth short-range repulsive, long-rang attractive potentials. We are working of rigorously proving the nonlinear stability of some of these states, in particular those supported on a finite set. To do so we exploit the gradient flow structure of the equation. The interesting issue is how to formulate the linearized problem in a proper way to account for all the perturbations of the steady state, in particular those that spread a measure which has a point concentration.
This is a project with Lijiang Wu. We study the equations in the case that the mobility of individuals depends on their location and allow for the presence of environmental boundaries. The space dependent mobility gives a Riemannian structure to the underlying space which leads us to study the equations on manifolds. This raises a number of challenges but also gives rise to new and interesting phenomena. Namely if for example there is a swarm affected by a unidirectional potential (say the individuals all know/feel where the food is) in the homogeneous environment this results in an orderly translation, while in some natural heterogeneous environments this leads to rolling swarms, not unlike those seen in swarming locust.
I have been interested in coarsening for about a decade. It started with a collaboration with Felix Otto and Tobias Rump on coarsening of droplets described by thin-film equations. I have since worked on ill-posed equations (with Selim Esedoglu), nonlocal interfacial problems, demixing of fluids (with Felix Otto and Christian Seis), and grain boundary networks and Voronoi diagrams (with Matt Elsey). Coarsening is the process in which patterns evolve in a way where typical shapes seen remain more-or-less the same, while the length scale of the system grows. Here are some examples: Left image shows early stage, right image a later stage; system size does not change from left to right.





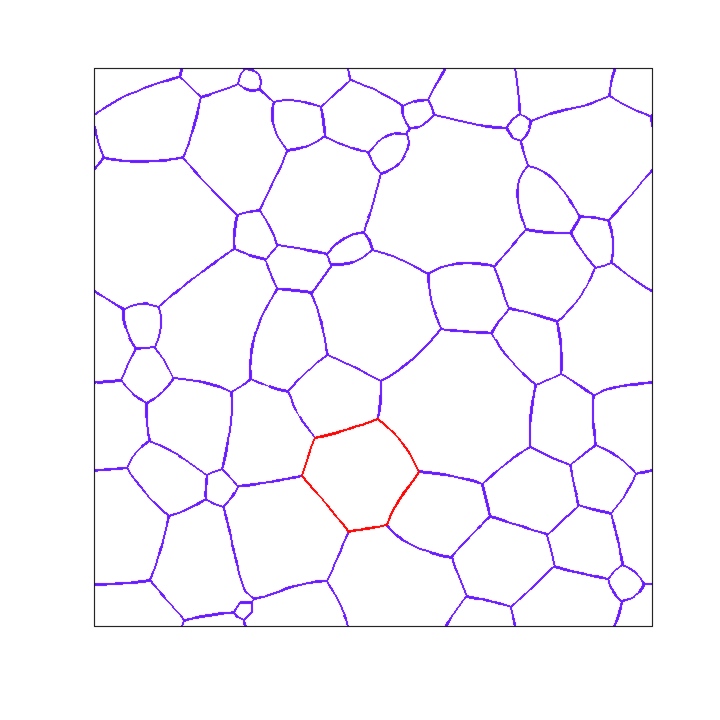
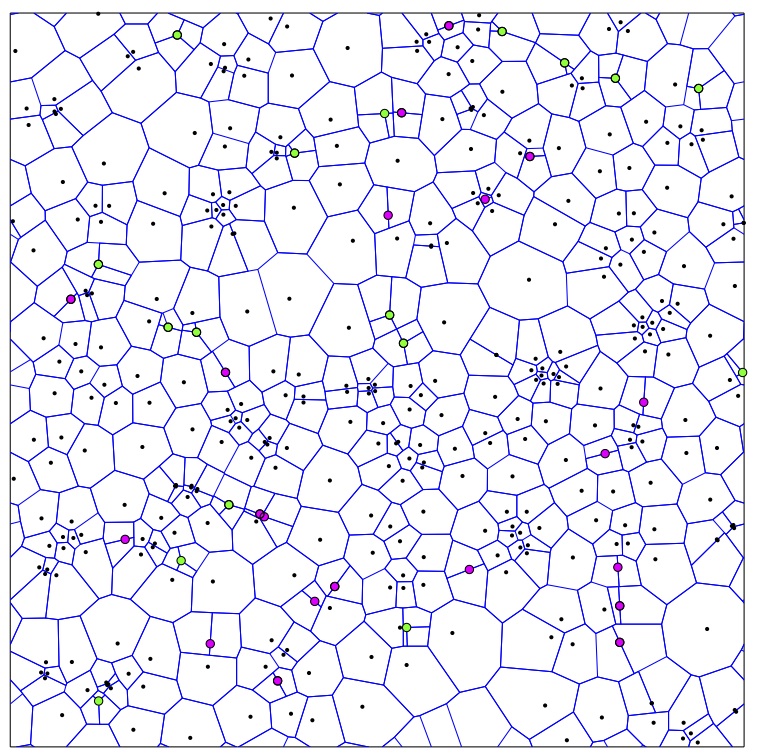
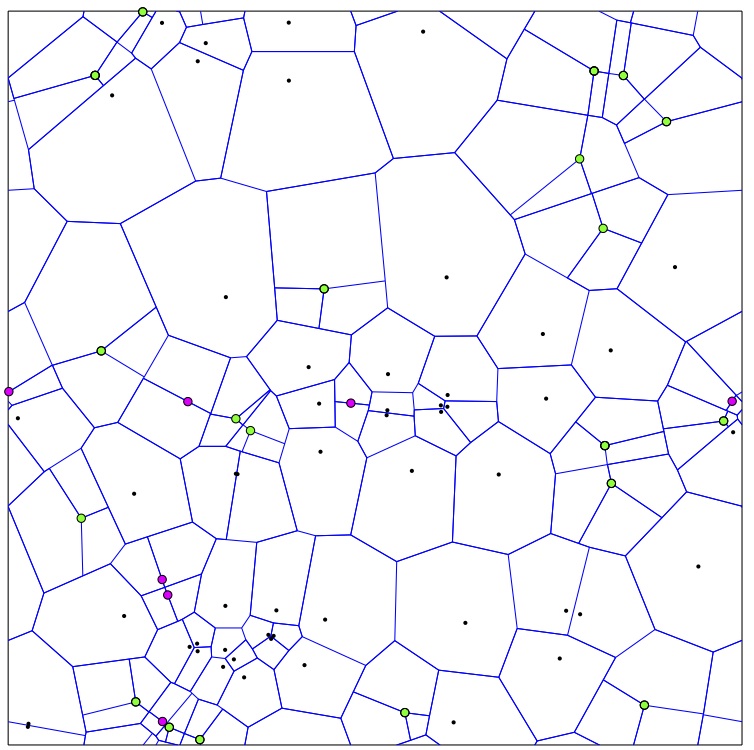
Most of the coarsening systems are energy driven, that is a free energy is being dissipated to move the system. The dissipation mechanism endows the configuration space with a geometric structure (the distance between two configurations squared is the minimal work needed to deform one configuration into other in unit time). Studying the energy landscape of the free energy in this geometry provides information about dynamics. In particular obtaining estimates on averaged slope of the energy provides estimates on the rate of coarsening.
Fall 2023
Course Description: The course will develop foundations of optimal transportation and investigate the properties of the
resulting
spaces. Dynamical description of optimal transport and variants, such as entropy regularized transport and unbalanced will also be
presented. We will cover a number of applications, in particular gradient flows in spaces of probability measures. The course will
include numerically computing optimal transportation maps, plans, and distances and statistical properties of approximating optimal
transportation in random setting. The material will be covered rigorously and rigorous arguments are expected on the homework. However
the course will be structures so that there will be options for some more applied assignments and projects.
Prerequisites: Knowledge of measure and integration and elements of: advanced real analysis (basics of Sobolev spaces), differential
equations, functional/convex analysis (Fenchel-Rockafellar duality), probability (Prokhorov compactness theorem), calculus of
variations (direct method, lower semicontinuity), and differential geometry (notion of differentiable manifold, tangent space, Riemann
metric).
- (with Andrew Warren) Nonlocal wasserstein distance: metric and asymptotic properties, (2022) preprint,
- (with Anna Korba and Lantian Xu) Accurate quantization of measures via interacting particle-based optimization, International Conference on Machine Learning (ICML) (2022) 24576-24595. published
- (with Jeff Calder and Sangmin Park) Boundary estimation from point clouds: algorithms, guarantees and applications, Journal of Scientific Computing 92 (2), (2022) 1-59. preprint, published
- (with Katy Craig and Nicolas Garcia Trillos) Clustering dynamics on graphs: from spectral clustering to mean shift through Fokker–Planck interpolation, In Active Particles, Volume 3, pp. 105-151, Birkhäuser (2022) preprint, published
- (with Francesco Patacchini) The nonlocal-interaction equation near attracting manifolds, Discrete & Continuous Dynamical Systems 42 (2), (2022) preprint, published
- (with Xin Yang Lu) Average-distance problem with curvature penalization for data parameterization: regularity of minimizers, ESAIM: Control, Optimisation and Calculus of Variations 27, (8), (2020), preprint, published
- (with Antonio Esposito, Francesco Patacchini, and Andre Schlichting) Nonlocal-interaction equation on graphs: gradient flow structure and continuum limit, Archive for Rational Mechanics and Analysis , 240 (2), (2021), 699-760. preprint, published
- (with Marco Carrocia and Antonin Chambolle) Mumford - Shah functionals on graphs and their asymptotics, Nonlinearity 33 (8), (2020) 3846 preprint, published
- (with Jeff Calder) Properly-weighted graph Laplacian for semi-supervised learning, Appl Math Optim 82 (3) (2019), 1111-1159. preprint, published
- (with Yousuf Soliman and Keenan Crane) Optimal cone singularities for conformal flattening, ACM Transactions on Graphics 37, no. 4, (2018), article 105, pages 1-17, preprint, published
- (with Matthew Dunlop, Andrew Stuart, and Matthew Thorpe) Large data and zero noise limits of graph-based semi-supervised learning algorithms, Applied and Computational Harmonic Analysis (2019) preprint, published
- (with Nicolás García Trillos, Moritz Gerlach, and Matthias Hein) Error estimates for spectral convergence of the graph Laplacian on random geometric graphs towards the Laplace--Beltrami operator, Found Comput Math (2019), preprint, published
- (with Matthew Thorpe) Analysis of p-Laplacian regularization in semi-supervised learning, SIAM J. Math. Anal. 51 (3), 2085-2120, preprint, published.
- (with Matthew Thorpe, Serim Park, Soheil Kolohuri, and Gustavo Rohde) A transportation $L^p$ distance for signal analysis, Journal of Mathematical Imaging and Vision 59 no. 2 (2017) pages 187-210, preprint , published
- (with Soheil Kolohuri, Serim Park, Matthew Thorpe, and Gustavo Rohde) Optimal mass transport: Signal processing and machine-learning applications, IEEE signal processing magazine 34 no. 4 (2017) pages 43-59, preprint , published
- (with Jian-Guo Liu and Bob Pego) Least action principles for incompressible flows and optimal transport between shapes, Calculus of Variations and Partial Differential Equations 58 (5), 179 preprint, published
- (with Nicolás García Trillos, and James von Brecht) Estimating perimeter using graph cuts, Advances in Applied Probability 49 no. 4, (2017) pages 1067-1090, preprint, published
- (with Slav Kirov) Multiple penalized principal curves: analysis and computation, Journal of Mathematical Imaging and Vision 59 no. 2 (2017) pages 234-256,, preprint published
- (with Nicolás García Trillos) A variational approach to the consistency of spectral clustering, Applied and Computational Harmonic Analysis 45 no. 2, (2018), pages 239-281, preprint, published
- (with Nicolás García Trillos, James von Brecht, Thomas Laurent and Xavier Bresson) Consistency of Cheeger and ratio graph cuts, Journal of Machine Learning Research, 17, no. 181, (2016), pages 1- 46. preprint, published
- (with Xin Yang Lu) Average-distance problem for parameterized curves, ESAIM: Control, Optimisation and Calculus of Variations, Vol. 22 no. 2 (2016), pages 404-416. preprint published
- (with Nicolás García Trillos) On the rate of convergence of empirical measures in infinity transportation distance, Canadian Journal of Mathematics, 67 (2015) pages 1358-1383. preprint published
- (with Robert Simione and Ihsan Topaloglu) Existence of ground states of nonlocal interaction energies, Journal of Statistical Physics, Vol. 159, Issue 4, (2015), pages 972-986. preprint published
- (with José Antonio Carrillo and Lijiang Wu) Nonlocal interaction equations on uniformly prox-regular sets, Discrete and Continuous Dynamical Systems A, Vol. 36, No. 3, (2016), pages 1209 - 1247. preprint published
- (with Nicolás García Trillos) Continuum limit of total variation on point couds, Arch. Ration. Mech. Anal., Vol. 220, No. 1, (2016), pages 193-241. preprint, published
- (with Lijiang Wu) Nonlocal interaction equations in environments with heterogeneities and boundaries, Communications in Partial Differential Equations, Vol. 40, No. 7, (2015), pages 1241-1281. preprint, published
- (with Matt Elsey) Mean-curvature flow of Voronoi diagrams, Journal on Nonlinear Science , Vol. 25 No. 1 (2015), pages 59-85. preprint, published
- (with Xin-Yang Lu) Properties of minimizers of average-distance problem via discrete approximation of measures, SIAM J. Math. Anal. , Vol 45, No. 5, (2013) 3114-3131. preprint, published
- Counterexample to regularity in average-distance problem, Ann. Inst. H. Poincare Anal. Non Lineaire, Vol 31, No. 1, (2014) 169-184, preprint, published.
- (with Wei Wang, Saurav Basu, John Ozolek, and Gustavo K. Rohde ) A linear optimal transportation framework for quantifying and visualizing variations in sets of images, International Journal of Computer Vision, Vol. 101, No. 2, (2013), 254-269, published
- (with Felix Otto and Christian Seis) Crossover of the coarsening rates in demixing of binary viscous liquids, Communications in Mathematical Sciences, Vol. 11, No. 2, (2013), 441-464, preprint, published.
- (with José Antonio Carrillo, Marco Di Francesco, Alessio Figalli, and Thomas Laurent) Confinement in nonlocal interaction equations, Nonlinear Analysis, 75, No. 2, (2012), 550-558, preprint, published
- (with Wei Wang, John Ozolek, Ann Lee, C. Chen, Gustavo K. Rohde) An optimal transportation approach for nuclear structure-based pathology, IEEE Trans. Med. Imaging. 30, no. 3 (2011) 621 - 631 published
- (with José Antonio Carrillo, Marco Di Francesco, Alessio Figalli, and Thomas Laurent) Global-in-time weak measure solutions, finite-time aggregation and confinement for nonlocal interaction equations, Duke Math. J. 156, (2011),no. 2, 229-271. preprint, published
- (with Andrea Bertozzi) Existence and uniqueness of solutions to an aggregation equation with degenerate diffusion, Commun. Pure Appl. Anal. 9 No. 6 (2010) pp.~ 1617-1637. preprint, published
- (with José Antonio Carrillo, Stefano Lisini, and Giuseppe Savaré) Nonlinear mobility continuity equations and generalized displacement convexity, J. Funct. Anal. 258 (2010) pp. 1273-1309, preprint, published
- (with José Antonio Carrillo) Example of a displacement convex functional of first order, Calc. Var. and PDE 36 (2009) pp. 547-564. preprint, published
- (with Selim Esedoglu) Refined upper bounds on the coarsening rate of discrete, ill-posed diffusion equations, Nonlinearity 21 (2008) pp. 2759-2776. preprint, published
- Coarsening in nonlocal interfacial systems, SIAM J. Math. Anal. 40, No. 3, (2008) pp. 1029-1048. preprint, published
- (with Karl Glasner, Felix Otto, and Tobias Rump) Ostwald ripening of droplets: The role of migration, European Journal of Applied Mathematics 20, No 1, (2009) pp. 1-67. preprint, published
- (with Robert McCann) Second-order asymptotics for the fast-diffusion equation, Internat. Math. Res. Notices (2006), Art. ID 24947, pp. 1-22. preprint, published
- (with Felix Otto and Tobias Rump) Coarsening rates in a droplet model: rigorous upper bounds, SIAM J. Math. Anal. 38, No. 2, (2006), pp. 503-529. preprint, published
- Linear stability of selfsimilar solutions of unstable thin-film equations, Interfaces and Free Boundaries, (2009) no. 3 pp. 375-398. preprint, published
- (with Mary C. Pugh) Selfsimilar blowup of unstable thin-film equations, Indiana Univ. Math. J. 54 (2005) no. 6 pp. 1697-1738. preprint, published
- (with Francesca da Lio and Inwon C. Kim) Nonlocal front propagation problems in bounded domains with Neumann-type boundary conditions and applications, Asymptotic Analysis 37 (2004) no. 3-4 pp. 257-292. preprint, published
- On level-set approach to motion of manifolds of arbitrary codimension, Interfaces and Free Boundaries, 5 (2003) pp. 417-458. published
- Aproximation schemes for propagation of fronts with nonlocal velocities and Neumann boundary conditions, Nonlinear Analysis, 52 (2003) pp. 79-115. published
