for a typical day in class.

Discrete Mathematics, 21-228

Carnegie Mellon University
Department of Mathematics
Summer Session II, 2000
M-F 1:30-2:50pm Wean 6423

• Final Exam due Th 8/10 by 1:00pm
  
• Schedule
  
• Exercises
  
• Practice problems
  
• Resources
  • Eric Weisstein's World of Mathematics
    A huge hyperlinked dictionary of mathematics -- highly recommended
  • Ian Stobert's Graph Theory site
    Includes many links to graph theory tutorials, notes, exercises, and open problems
    

Instructor: Ojas Parekh
E-mail: odp@cmu.edu
Office: Physical Plant 342 (Exit Wean 1st Floor, cross the street, and take a left onto the sidewalk. Continue on sidewalk until patio area and follow "Math Dept." sign.)
Office Phone: x8-1447
Home Phone: 421-3944
Office Hours: M-F 3-4pm and by appointment

Prerequisites:
The most important and only real prerequisite is (mathematical) curiousity. We can shape this to fill just about any other prerequisite. Exposure to a "ransition to modern math" course such as 15-127 or 21-127 is helpful but not absolutely necessary. Please contact me if you have any doubts about your qualifications.

Course Description:
The emphasis of this course will be on solving problems, and this is what we and you will spend a significant amount of time doing. Along the way we will meander through many of the topics typically presented in an introductory discrete math course as well as some that are overlooked by such a course. We will try to focus on problems that are easy to state, require creative application of course concepts, have elegant but not necessarily simple solutions, and most importantly, are fun to solve.

We will aim to replace lecturing by deriving the material together whenever possible.I n the process you will sharpen your communication and collaborative thinking skills. In fact, thanks to modern technology, we will enter at least one problem-solving contest on the internet and see how we fare as a class during our six week stint.

I will enjoy the course, and I will do all I can to ensure you will as well!

Schedule and Topics:
A complete schedule including topics, readings, assignments, internet resources, and exams will be maintained on the course website at http://www.math.cmu.edu/~odp/DiscreteN00. The selection of topics we will cover is flexible and student feedback is welcome.

(You can get ghostscript, a postscript interpreter, at http://www.cs.wisc.edu/~ghost .)

Date	Topic	Reading	Exercises	Homework
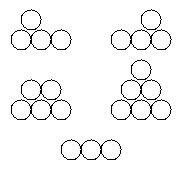
W, 7/5	3 ways to color balls	Frieze's notes Rosen §§4.1, 4.6; Roman §§4.4-4.6
Th, 7/6	Relearning to count: permutations, combinations, and binomial coefficients	Frieze: Counting 251 notes: Count without counting Rosen §§4.3, 4.6; Roman §§4.4-4.6	Ex1
F, 7/7	Binomal coeffs, indentities, and _the_ theorem	Frieze: Binomial coeffs 251: Flexing your counting... 251: Polynomials that count Rosen §4.6; Roman §§4.7 & 5.2	Ex2	Hw1 due T, 7/11
M, 7/10	Multinomial coefficients Pigeonhole principle	Frieze: Multinomial coeffs Frieze: Pigenhole principle Rosen §4.2; Roman §§4.3, 4.8, 5.1	Ex3
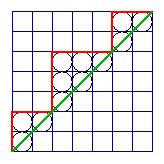
T, 7/11	Grid-path problems and Catalan #s	Frieze: Grid-path problems Exercises on Catalan and related #s	Ex4	Hw1 due
W, 7/12	Fibonacci and friends	251: A number you can... Rosen §5.1; Roman §4.9	Ex5	Hw2 due M, 7/17
Th, 7/13	Solving linear recurrences	Frieze: Linear recurrences Rosen §§5.2 & 5.3; Roman §4.10 & 4.11	Ex6
F, 7/14	Solving (nonhomogeneous) recurrences	Frieze: Linear recurrences(same as above) Roman §4.12
Su, 7/16	Problem session 7:00pm, room tba
M, 7/17	Recurrences for partition problems, permutations, derangements, and triangulations	Frieze: Permutations Frieze: Partition recurrences Frieze: Triangulations and gfs	Ex7	Hw2 due Hw3 due F, 7/21
T, 7/18	To exclude or not to exclude...	Frieze: Inclusion-exclusion 251: To exclude or not to exclude Rosen §§5.4 & 5.5; Roman §§5.5-5.7
W, 7/19	Exam 1 (solutions)	Exam 1 sample problems Solutions for above
Th, 7/20	Intro to discrete probability: Monty Hall problem and Birthday paradox	Frieze: Intro to descrete prob. 251: Probability Rosen §4.4
F, 7/21	Conditional probability and pitfalls	Frieze: Conditional probability Frieze: Boole's inequality & 2-coloring a set system 251: Probability pitfalls Rosen §4.5		Hw3 due Hw4 due T, 7/25
M, 7/24	Random variables and expectation Graph Theory	Frieze: Random variables 251: Great Expectations Rosen §§4.5 & 7.1
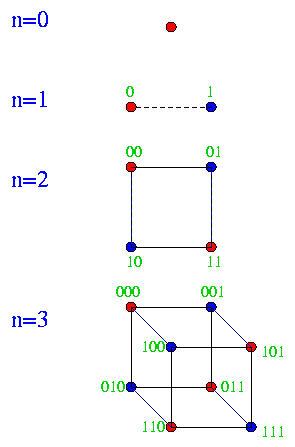
T, 7/25	Graph Thoery: Definitions, representations, and isomoprhisms	Frieze: Intro Graph Theory 251: Graph Theory Rosen §§7.2 & 7.3	Ex8	Hw4 due Hw5 due F, 7/28
W, 7/26	Paths and walks	Frieze: Paths and walks 251: Blowing in the wind Rosen §7.4	Ex9
Th, 7/27	Graph forestry: trees	Frieze: Trees Rosen §7.4, §§8
F, 7/28	Guest Lecture: Coloring Euler's Plane by Goeff Atkinson	251: Planar graphs Rosen §7.7		Hw5 due Hw6 due T, 8/1
M, 7/31	Euler, Euler, he's our man...	Frieze: Eulerian graphs Rosen §7.5
T, 8/1	De Bruijn Graphs, the Chinese Postman Problem, and matchings	Frieze: Matchings 251: Math of 1950's dating	Ex10	Hw6 due (solutions) Hw7 due F, 8/4
W, 8/2	Problem Day
Th, 8/3	Exam 2 (solutions)	Exam 2 sample problems Solutions for above
F, 8/4	Review: Exam 2 solutions, matchings, and vertex covers			Hw7 due (solutions) Extra Credit due Th, 8/10
M, 8/7	Review: Hw7 solutions, derangements, and even permutations
T, 8/8	Cryptography: The RSA cryptosystem	An intro to cryptography RSA Labs crypotgraphy FAQ RSA lecture slides		Final Exam due Th 8/10 by 1:00pm
W, 8/9	Error-Correcting codes

Texts:
Much of the material we will be covering appears in

Discrete Mathematics and its Applications, by K. H. Rosen, published by McGraw-Hill (3rd edition or later).
An Introduction to Discrete Mathematics, by S. Roman, published by HBJ.
Applied Combinatorics, by A. Tucker, published by Wiley & Sons.

I recommend you get at least one of the books above or a suitable substitute (Bogart). Rosen explores the topic from a computer science point of view while the latter two are more traditional. When a course topic does not appear in an introductory discrete math text, I will provide (pointers to) handouts. I also recommend,

How To Solve It: A New Aspect of Mathematical Method, by G. Polya.

Used copies of these books can be bought for as little as $5 through sites such as http://half.com/ and http://www.abe.com/. If you prefer a new copy, I suggest consulting http://addall.com/.

Assignments and Exams:
As this is a problem-solving course, students will be expected to solve (plenty of) problems. In addition to readings, an exercise set consisting of 2-5 routine exercises will be assigned daily. A corresponding number of students will be selected randomly each day to present the previous day's exercises, each individual earning up to 10 points. Students must complete these exercises without collaboration. If a student is not present when selected to present, he will receive a score of 0. We will devise a system to ensure the fairness of this process. Problem sets consisting of more challenging problems will be assigned weekly. Collaboration on the problem sets is encouraged; however, each student must clearly list all individuals (s)he has consulted. Late problem sets will be accepted with a penalty of a letter grade per day tardy.

It is also important that each student be able to solve homework problems on her own as no collaboration is permitted on the exams. I take academic honesty very seriously, and the school's policy on this matter will be strictly enforced. There will be up to 3 exams and a final exam depending upon the topics we cover. Students may opt to replace at most one exam with a project chosen jointly with the instructor or by presentation of one of the class topics. Make-up exams will only be given in extreme circumstances and will be oral. I encourage anyone with special needs to discuss them with me so we may accommodate them.

Grading:
The tentaive grading scale will be:

A: [100, 90]
B: (90, 80]
C: (80, 70]
D: (70, 60]
R: (60, 0]

If the scale is modified at all, it will only be done in the students' favor. Homeworks will count for at least 25%, and the final will count for no more than 25%

---

Exercises

Thu, 7/6
1. What is lim_{n -> inf} C(n-1+k,k)/C(n,k), where C(n,k) = n!/(k!*(n-k)!)?
2. How many ways can the letters of "discrete" be rearranged?
3. What fraction of initial blackjack deals are blackjacks (A & {10,J,Q,K})?
4. The digits of how many 3-digit numbers sum to 9?

Solutions
1. C(n-1+k,k) and C(n,k) are both polynomials of degree k in n with a coefficient of 1 for the n^k term (i.e. n^k + an^(k-1) + ...), so the limit goes to 1.

2. There are 8! ways of arranging the letters if they were all different, but since the 2 'e's are identical, we are counting each rearrangement twice, so we have 8!/2 total.

---

Fri, 7/7
1. For how many 2-subsets {1,2,3,...,2n} is the sum of the 2 elements even?
2. Prove C(2n, 2) = 2*C(n, 2) + n^2 both algebraically and combinatorially.

Solutions
1. The 2-set's sum will be even if both elements are even or both are odd. There are n even elements and n odd elements, so there are C(n,2) 2-sets with both elements odd and C(n,2) 2-sets with both even, for a total of 2*C(n,2) = n(n-1). Alternatively, there are C(2n,2) sets in total and exactly n^2 (pick 1 element from the n even and 1 from the n odd) will have an odd sum.

2. From above, C(2n,2) - n^2 = 2*C(n,2), or you can break the 2n elements into 2 groups of n. 2*C(n,2) counts ways of picking elements from the same group, and n^2 counts ways of picking one element from each group.

---

Mon, 7/10
1. Show that at a party with at least 2 people, there are 2 people who have shaken the same number of hands.
2. What is the coefficient of (w^2)(x^2)(y^2)(z^2) in the expansion of (w + x + y + z)^8?
3. In how may ways can one divide the set {a,b,c,d,e,f} into three mutually disjoint subsets A, B, C where A has size 3, B has size 1, and C has size 2?
*4. We have 30 boys and 30 girls going on a school trip on the big cheese. The cheese has 30 seats, each of which seats 2 people. Let's say this is a 2nd grade class and girls want to sit with girls and likewise for boys. How many ways of accomplishin this if the seat in which each kid sits matters? What if order only matters for girls? What if only the seat (and not which of the 2 positions on that seat) matters?

Solutions
1. Each person can shake between 0 and n-1 hands, but note that if someone shakes n-1 hands than no one can have shaken 0 hands, so either the number of hand shakes falls in {0, ..., n-2} or {1, ..., n-1}. There are n-1 possible values in either case, so the pigeonhole principle gives us that 2 of the n people must have shaken the same number of hands.

2. Using the multinomial theorem or counting using the expansion: 8!/(2!2!2!2!).

3. We can represent each partition of {a,b,c,d,e,f} as a permutation of length 6 of the characters {A,A,A,B,C,C} to denote the set in which each element belongs. For examle if A = {a,b,c}, B = {c}, and C = {e,f} then our permutation would be AAABCC. We find the total number is 6!/(3!1!2!).

4. First let's pick the seats for the boys (and girls). There are C(30, 15) ways of doing this. Now we order the boys and the girls, so we get C(30, 15)*30!*30!. If order only matters for the girls then we "only" have C(30, 15)*30! distributions. If the position on each seat doesn't matter than we can unorder the pairs on each seat by dividing by the 2 ways you can put 2 people on one seat for each seat, yielding C(30, 15)*30!*30!/2^30.

---

Tue, 7/11
1. Exhibit a bijection between the following problems and monotone grid paths from (0, 0) to (a, a) [for appropriate choice of a] that touch or lie above the line x=y.
i. sequences of n +1's and n -1's such that every partial sum (sum of positions 1,2,...,k for k=1...2n) is nonnegative

For n=3: +++---, ++-+--, ++--+-, +-++--, +-+-+-

ii. coin stackings on n adjacent coins such that each coin rests on exactly two coins

For n=3:
2. Show that if a_1 + a_2 + ... + a_n - n + 1 balls are distributed in n bins, where a_i >= 1 for all i, then there is some bin j which contains at least a_j balls. [Hint: Suppose bin i contains less than a_i balls for all i ...]

Solutions
1. i. Let a +1 represent moving up and -1 represent moving right. A sequence of n +1's and n -1's represents a path from (0, 0) to (n, n). Since the partial sums are all positive, we'll have at least as many up as right moves, so we'll be on or above the line y=x.

ii.

2. Suppose bin i contains less than a_i balls for every i, so bin i contains <= a_i - 1 balls for each i. We sum all these up and get that there must be at most (a_1 - 1) + (a_2 - 1) + ... + (a_n - 1) = a_1 + ... + a_n - n balls, but this is a contradiction since we distributed a total of a_1 + ... + a_n - n + 1 balls. How can we restate this as a pigeonhole principle proof?

---

Wed, 7/12
1. Determine recurrences for the following types of strings of length n:
i. binary with an even number of 0s [solve this one]
ii. ternary (over {0,1,2}) with an even number of 0s [solve]
iii. quaternary (over {0,1,2,3}) with an even number of 0s

[Hint: For part ii guess that b_n = a*3^n + b, for some constants a & b. Plug this guess into the recurrence and see what happens.]

Solutions
1. i. Let's fix the 1st position and see what happens:
1|< n-1 >: we want the stuff in the < n-1 > to be a string with an even number of 0s, but we know that's a_{n-1}.
0|< n-1 >: we want the stuff in the < n-1 > to be a string with an odd number of 0s. We know how many total string we have of length n-1, 2^(n-1), and we know how many have an even number of 0s, a_{n-1}, so there must be 2^(n-1)-a_{n-1} with an odd number of 0s.
Every string falls into exactly one of the two cases above, so we have
a_{n-1} + (2^(n-1) - a_{n-1}) = 2^(n-1) such strings. The recurrence actually solved itself!

ii. We'll play the same game:
1|< n-1 >
2|< n-1 >: in each of these two cases we want < n-1 > to be a ternary string of length n-1 with an even # of 0s, so we have b_{n-1} ways for each of these cases
0|< n-1 >: how many ternary string of length n-1 with an odd # of 0's? We know that's all of 'em minus the bad (even) ones, 3^(n-1) - b_{n-1}.

In total we have b_n = 2*b_{n-1} + (3^(n-1) - b_{n-1}) = 3^(n-1) + b_{n-1}. Guessing b_n = a*3^n + b gives us:
a*3^n + b = 3^(n-1) + (a*3^(n-1) + b) =>
3a*3^(n-1) + b = (1+a)*3^(n-1) + b =>
3a = 1 + a => a = 1/2

What about b? We need it to sync our sequence with the initial conditions. How many strings of length 0 have an even # of 0s? The empty string has 0 0's, which is fine, so b_0 = 1. We found b_n = 1/2*3^n + b from above, so 1 = b_0 = 1/2 + b => b = 1/2.

Our final solution is b_n = 1/2*3^n + 1/2. We can compute a few values to check our work. 1 = b_0 = 1/2 + 1/2 and 2 = b_1 = 3/2 + 1/2 work!

iii. Beating a few (dead?) horses, c_n = 4^(n-1) + 2c_{n-1} and c_0 = 1. We'll explore the solution of this type of recurrence in the next few sessions.

---

Thu, 7/13
1. Solve the following recurrences:
i. s_n = s_{n-1} + 6s_{n-2}, s_0 = 0, s_1 = 1
ii. s_n = s_{n-1} + 6s_{n-2}, s_0 = 1, s_1 = 0
iii. s_n = 4s_{n-1} - 4s_{n-2}, s_0 = -2, s_1 = 2
iv. s_n = 2s_{n-2}, s_0 = 1, s_1 = 5
v. s_n = -2s_{n-2}, s_0 = 1, s_1 = 5

Make sure you check your work.

Solutions
1. i. Our characteristic equation is r^2 - r - 6 = 0, so our roots are r_1 = 3 and r_2 = -2, which gives us a solution of s_n = c_1*3^n + c_2*(-2)^n. Using the initial conditions:

0 = s_0 = c_1 + c_2 => c_1 = -c_2
1 = s_1 = 3*c_1 - 2*c_2,

so our solution is c_1 = 1/5, c_2 = -1/5, hence s_n = 1/5*3^n - 1/5*(-2)^n.

Of course we would never quit without checking our work, so we find s_0 = 1/5 - 1/5 = 0, and s_1 = 3/5 + 2/5 = 1.

ii. We have the same characteristic equation as above, so s_n = c_1*3^n + c_2*(-2)^n. Note that s_0 > s_1; this is perfectly fine. This time our initial conditions give us:

1 = s_0 = c_1 + c_2 => c_2 = 1 - c_1
0 = s_1 = 3*c_1 - 2*c_2,

so our solution is c_1 = 2/5, c_2 = 3/5 => s_n = 2/5*3^n + 3/5*(-2)^n. We check that s_0 = 2/5 + 3/5 = 1 and s_1 = 6/5 - 6/5 = 0.

iii. Our characteristic equation is r^2 - 4r + 4 = 0, and our only root is r = 2; however, since we have a second order recurrence, in the worst case (depends on initial conditions) we'll need to combine two linearly independent solutions. We showed in class that if r^n is a solution then c*n*r^n is also solution, so we can use both of these. Thus

s_n = c_1*r^n + c_2*n*r^n.

Our intial conditions give us:

-2 = s_0 = c_1 + 0 (that was easy)
2 = s_1 = 2*c_1 + 2*c_2

We get c_1 = -2, c_2 = 3, and s_n = -2*2^n + 3*n*2^n = 3*n*2^n - 2^(n+1). It's our duty to check s_0 = -2 and s_1 = 3*2 - 4 = 2.

iv. We only have two terms here, but note that the difference between the highest and loest indexed terms is 2, so this is indeed a 2nd order recurrence. Our characteristic equation is r^2 = 2, so we have s_n = c_1*sqrt(2)^n + c_2*(-sqrt(2))^n.

1 = s_0 = c_1 + c_2
5 = s_1 = c_1*sqrt(2) - c_2*sqrt(2)

Some work gets us c_1 = (2 + 5*sqrt(2))/4, c_2 = (2 - 5*sqrt(2))/4, and s_n = (2 + 5*sqrt(2))/4 * sqrt(2)^n + (2 - 5*sqrt(2))/4 * (-sqrt(2))^n. Checking... s_0 = (2 + 5*sqrt(2))/4 + (2 - 5*sqrt(2))/4 = 1, and s_1 = (2 + 5*sqrt(2))/4 * sqrt(2) - (2 - 5*sqrt(2))/4 * sqrt(2) = 5.

v. Ouch, this time we have r^2 = -2, so s_n = c_1*(i*sqrt(2))^n + c_2*(-i*sqrt(2))^n [Note that i*r^n is not the same as (i*r)^n]. We have to solve the following mess:

1 = s_0 = c_1 + c_2
5 = s_1 = i*c_1*sqrt(2) - i*c_2*sqrt(2)

More than some work gets us c_1 = (2 - 5i*sqrt(2))/4, c_2 = (2 + 5i*sqrt(2))/4, and s_n = (2 + 5i*sqrt(2))/4 * (i*sqrt(2))^n + (2 - 5i*sqrt(2))/4 * (-i*sqrt(2))^n. Checking... s_0 = (2 - 5i*sqrt(2))/4 + (2 + 5i*sqrt(2))/4 = 1, and s_1 = (2 - 5i*sqrt(2))/4 * i*sqrt(2) - (2 + 5i*sqrt(2))/4 * i*sqrt(2) = 5.

---

Mon, 7/17
1. Work on the exam 1 sample problems. You will present Question 4, (d) (p. 8) tomorrow.

---

T, 7/25
1. Using rectangular blocks whose entries are all equal, write down an adjacency matrix for for K_{m,n}.

2. Show that the sum of the degrees of all the vertices in any undirected graph (multiple edges and loops are fine) is even.
[Hint: Appears in Frieze notes]

3. Let G be the graph whose vertex set is the set of binary strings of length n, with vertex x adjacent to vertex y iff x and y differ in exactly one position. What is a more common name for this graph when n = 0, 1, 2, and 3? Is this graph bipartite?

Solutions
1. K_{m,n} has m+n vertices so we'll divide the adjacency matrix into 4 blocks:


2. Each edge is counted exactly twice in the sum of the degrees, hence the sum of the degrees is equal to twice the number of edges, which is even.

3.One can apply induction according to pattern below to show that the graphs are bipartite (2-colorable).

---

Wed, 7/26
1.Prove that if G has at least one edge and no cycle, then G has a vertex of degree 1.

2.What is the chromatic number (the minumum number of colors required for a proper coloring) of the Petersen Graph. Can you prove that you've found the optimal coloring?

Solutions
1.Look at any maximal path P in G. Such a path exists since G has least one edge. Let u and v be the endpoints of P. The vertices u or v cannot be connected to some vertex not on P, since this would mean P wasn't maximal. On the other hand if u or v were connected to some vertex on P, G would have a cycle, hence u and v are vertices of degree 1. In this case we actually proved a stronger result -- G has two leaves.

2.A 3-coloring appears below. Note that this is optimal since the Petersen Graph is not bipartite.

---

Tuesday, 8/1
1. What's the size of a maximum matching in the Petersen Graph? Prove your solution is optimal.

2. Why can't one use a greedy algorithm to find a minimum cost perfect matching (like we did for the Chinese Postman Problem example in class)? In other words, suppose you're given a complete graph G = (V,E). The greedy algorithm simply selects the cheapest edge {u,v} in E, deletes u and v, and repeats the procedure until every vertex in V is matched.

Your task is to assign costs to the edges of some complete graph G in a way such that the greedy algorithm doesn't find the cheapest perfect matching. How much worse is the greedy algorithm's matching than the best one? How much worse can you make it?

Solutions
1. Take the 5 edges that connect the outer cycle to the star in the drawing of the petersen graph above. It is optimal since no one can do better than perfection.

2. The greedy algorithm would choose the red edges. It would have picked the edge of cost 1, but then it would be forced to choose the really expensive edge too, whereas the blue edges are a minimum cost perfect matching.