In this package, the user has four choices of symmetrizations resulting in four different search directions, namely,
;
, where N
is the unique matrix such that
,
and D is a diagonal matrix; and
,
where the matrices D and 
are defined as follows.
Suppose 
and 
are the Cholesky factorizations
of X and Z respectively. Let the SVD of 
be
. Let 
and 
be positive
diagonal matrices such that the equalities
and 
hold, with
all the rows of and 
having unit norms. Then
.
To describe our implementation 3, a discussion on the efficient computation of the Schur complement matrix M is necessary, since this is the most expensive step in each iteration of our algorithms where usually at least 80% of the total CPU time is spent. From equation (10), it is easily shown that the (i,j) element of M is given by
Thus for a fixed j, computing first the matrix 
and then taking inner product with each 
, 
,
give the jth column of M.
However, the computation of M for the four search directions
mentioned above can also be arranged in a different way.
The operator 
corresponding to
these four directions can be decomposed generically as
where 
denotes the Hadamard (elementwise) product
and the matrices R, T, 
, and 
depend
only on X and Z.
Thus the (i,j) element of M in (14) can
be written equivalently as
Therefore the Schur complement matrix M can also be formed
by first computing and storing
for each 
,
and then taking inner products as in (15).
Computing M via different formulas, (14) or
(15), will result in different computational complexities.
Roughly speaking, if most of the matrices 
are dense, then
it is cheaper to use (15). However,
if most of the matrices are sparse, then
using (14) will be cheaper because
the sparsity of the matrices can be exploited
in (14) when taking inner products.
For the sake of completeness, in Table 1,
we give an upper bound on the complexity
of computing M for the above mentioned search directions
when computed via (14) and (15).
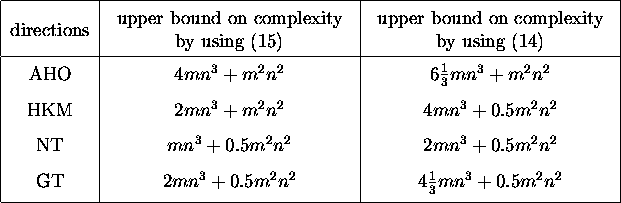
Table 1:
Upper bounds on the complexities
of computing M (for real SDP data) for various search directions.
We count one addition and one multiplication each as one flop.
Note that, except for the HKM direction, all the others require
an eigenvalue decomposition of a symmetric matrix in the
computation of M.
The reader is referred to [2], [8], and
[9] for more computational details, such as
the actual formation of M and 
,
involved in computing the above search directions.
The derivation of the upper bounds
on the computational complexities of M
computed via (14) and (15)
is given in [9].
The issue of exploiting the sparsity of the matrices
is discussed in full detail in [5]
for the HKM and NT directions; whereas an
analogous discussion for the AHO and GT directions
can be found in [9].
In our implementation, we decide on the formula to
use for computing M based on
the CPU time taken during the third and fourth
iteration to compute M
via (15) and (14), respectively.
We do not base our decision on the
first two iterations for two reasons.
Firstly, if the initial iterates 
and 
are
diagonal matrices, then the CPU time taken
to compute M during these two iterations
would not be accurate estimate of
the time required for subsequent iterations.
Secondly, there are overheads incurred when
variables are first loaded into
MATLAB workspace.
We should mention that the issue of exploiting the
sparsity of the matrices is not fully resolved
in our package. What we have used in our package is
only a rough guide. Further improvements on this
topic are left for future work.
