For later discussion, let us first introduce the
operator ![]() defined by
defined by
The adjoint of ![]() with respect to the standard inner products
in
with respect to the standard inner products
in ![]() and
and ![]() is the operator
is the operator
The main step at each iteration of our algorithms is the
computation of the search direction ![]() from the symmetrized Newton equation (with respect to
an invertible matrix P which is usually chosen as a function of the
current iterate X,Z) given below.
from the symmetrized Newton equation (with respect to
an invertible matrix P which is usually chosen as a function of the
current iterate X,Z) given below.
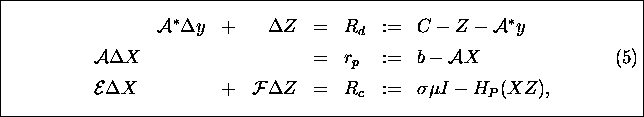 where
where ![]() and
and ![]() is the
centering parameter. Here
is the
centering parameter. Here
![]() is the symmetrization operator defined by
is the symmetrization operator defined by
and ![]() and
and ![]() are the linear operators
are the linear operators
where ![]() denotes the linear operator defined by
denotes the linear operator defined by
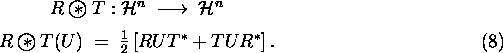
Assuming that ![]() , we compute the search direction via
a Schur complement equation as follows
(the reader is referred to [2] and [8] for details).
First compute
, we compute the search direction via
a Schur complement equation as follows
(the reader is referred to [2] and [8] for details).
First compute ![]() from the Schur complement equation
from the Schur complement equation
where
Then compute ![]() and
and ![]() from the equations
from the equations
If ![]() , solving (9) by a direct
method is overwhelmingly expensive;
in this case, the user should consider using an implementation that
solves (9) by an iterative method
such as CG or QMR.
In our package, we assume that
, solving (9) by a direct
method is overwhelmingly expensive;
in this case, the user should consider using an implementation that
solves (9) by an iterative method
such as CG or QMR.
In our package, we assume that ![]() and
(9) is solved by a direct method such
as LU or Cholesky decomposition.
and
(9) is solved by a direct method such
as LU or Cholesky decomposition.