

Next: The Mehrotra-type predictor-corrector algorithm
Up: Infeasible-interior-point algorithms
Previous: Computation of specific search
The algorithmic framework of our primal-dual path-following algorithm is
as follows.

Remarks.
- (a)
The adaptive choice of the step-length parameter
in (19) is used as the default in our implementation,
but the user has the option of fixing the value of
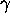 .
.
- (b)
It is known that as the parameter
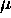 decreases to 0,
the norm
decreases to 0,
the norm 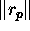 will tend to increase,
even if the initial iterate
is primal feasible, due to increasing numerical
instability of the Schur complement approach.
In our implementation of the algorithms, the user has the option of
correcting for the loss in primal feasibility by projecting
will tend to increase,
even if the initial iterate
is primal feasible, due to increasing numerical
instability of the Schur complement approach.
In our implementation of the algorithms, the user has the option of
correcting for the loss in primal feasibility by projecting 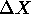 onto the null space of the operator
onto the null space of the operator 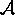 .
That is, before updating to
.
That is, before updating to 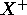 , we replace
, we replace 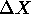 by
by
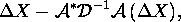
where 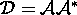 . Note that this
step is inexpensive. The
. Note that this
step is inexpensive. The  matrix
matrix 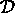 need only to be formed once at the beginning of
the algorithm.
need only to be formed once at the beginning of
the algorithm.
- (c)
We only described termination when approximately optimal solutions
are at hand. Nevertheless, our codes stop when other indications
arise. For example, if the step makes little progress, or if the
step-length taken in either primal or dual spaces becomes very small,
we terminate. We also stop if we get an indication of infeasibility.
For example, if the current iterate has
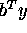 much larger than
much larger than
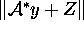 , then a suitable scaling is an approximate
solution of
, then a suitable scaling is an approximate
solution of 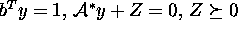 , which
is a certificate that the primal problem is infeasible.
Similarly, if
, which
is a certificate that the primal problem is infeasible.
Similarly, if 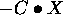 is much larger than
is much larger than 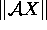 ,
we have an indication of dual infeasibility: a scaled iterate is then
an approximate solution of
,
we have an indication of dual infeasibility: a scaled iterate is then
an approximate solution of 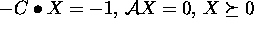 , which is a certificate that the dual problem
is infeasible. In either case, we return
the appropriate scaled iterate suggesting primal or dual infeasibility.
, which is a certificate that the dual problem
is infeasible. In either case, we return
the appropriate scaled iterate suggesting primal or dual infeasibility.

![]() . Note that this
step is inexpensive. The
. Note that this
step is inexpensive. The ![]() matrix
matrix ![]() need only to be formed once at the beginning of
the algorithm.
need only to be formed once at the beginning of
the algorithm.