Let ![]() be the operator
be the operator
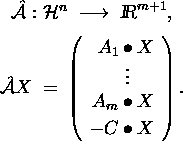
Then the adjoint of ![]() with respect to the standard inner products
in
with respect to the standard inner products
in ![]() and
and ![]() is the operator
is the operator
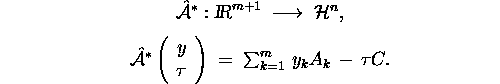
Our homogeneous and self-dual linear feasibility model for SDP is based on those appearing in [11] for linear programming (LP). It has the following form:
where ![]() are positive semidefinite. A solution to this system
with
are positive semidefinite. A solution to this system
with ![]() positive either gives optimal solutions to the SDP and
its dual or gives a certificate of primal or dual infeasibility.
positive either gives optimal solutions to the SDP and
its dual or gives a certificate of primal or dual infeasibility.
At each iteration of our algorithms, we apply Newton's method to a perturbation of equation (22), namely,
where the right-hand side quantities are considered as fixed.
Here ![]() and
and ![]() are parameters, and
are parameters, and ![]() and
and ![]() are
defined in (26) and (25) below, respectively.
are
defined in (26) and (25) below, respectively.
Just as in the case of infeasible path-following methods,
the search direction
![]() at each iteration of our homogeneous algorithms
is computed from a symmetrized Newton equation
derived from the perturbed equation (23):
at each iteration of our homogeneous algorithms
is computed from a symmetrized Newton equation
derived from the perturbed equation (23):
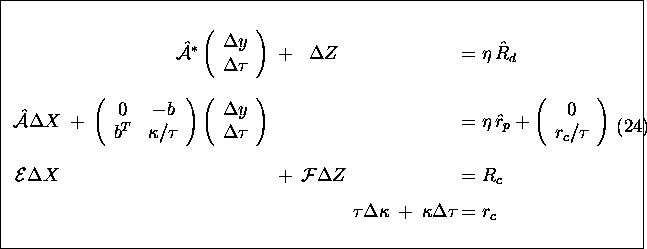 where
where ![]() and
and ![]() ,
, ![]() are defined as in (6)
and (7), respectively, and
are defined as in (6)
and (7), respectively, and
We compute the search direction via a Schur complement
equation as follows. First compute ![]() from the
equation
from the
equation
where
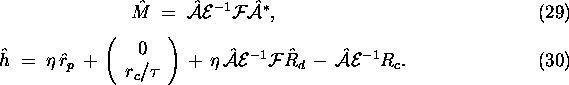
Then compute ![]() ,
, ![]() , and
, and ![]() from the equations
from the equations