The main routine

 

The main routine that corresponds to the infeasible path-following algorithms described in Section 2 is sdp.m:

  [obj,X,y,Z,gaphist,infeashist,pathreshist,info] 
     = sdp(blk,A,C,b,X0,y0,Z0),
 

whereas the corresponding routine for the homogeneous self-dual algorithms described in Section 3 is sdphlf.m:

  [obj,X,y,Z,gaphist,infeashist,pathreshist,info] 
     = sdphlf(blk,A,C,b,X0,y0,Z0). 
 

Functions used.
sdp.m calls the following function files during its execution:

 
AHOpred.m        HKMpred.m       NTpred.m        GTpred.m

AHOcorr.m  	 HKMcorr.m  	 NTcorr.m  	 GTcorr.m

trace.m    	 Asum.m     	 cholaug.m  	 aasen.m

Atriu.m   	 pathres.m  	 corrprim.m 	 steplength.m

scaling.m.

sdphlf.m calls the same set of function files except that the first two rows in the list above are replaced by

 
AHOpredhlf.m     HKMpredhlf.m    NTpredhlf.m      GTpredhlf.m

AHOcorrhlf.m  	 HKMcorrhlf.m    NTcorrhlf.m   	  GTcorrhlf.m.

In addition, sdphlf.m calls the function file schurhlf.m.

C Mex files used.
The computation of the Schur complement matrix M requires repeated computation of matrix products involving either matrices that are triangular or products that are known a priori to be hermitian. We compute these matrix products in a C Mex routine generated from a C program mexProd2.c written to take advantage of the structures of the matrix products. Likewise, computation of the inner product between two matrices is done in a C Mex rountine generated from a C program mextrace.c written to take advantage of possible sparsity in either matrix. Another C Mex routine that is used in our package is generated from the C program mexaasen.c written to compute the Aasen decomposition of a hermitian matrix [1]. To summarize, here are the C programs used in our package:

mextrace.c  mexProd2.c	 mexaasen.c

Input arguments.

blk: a cell array describing the block structure of the 's and C (see below).

A : a cell array with m columns such that the kth column corresponds to the matrix .

C, b: given data of the SDP.

X0, y0, Z0: an initial iterate.

Output arguments.

obj = [ ].

X,y,Z: an approximately optimal solution.

gaphist: a row vector that records the duality gap at each iteration.

infeashist: a row vector that records the infeasibility measure at each iteration.

pathreshist: a row vector that records the centrality measure at each iteration.

info: a vector that contains performance information:

info(1) = termination code,
info(2) = number of iterations taken,
info(3) = final duality gap,
info(4) = final infeasibility measure, and
info(5) = total CPU time taken.

info(1) takes on nine possible integral values depending on the termination conditions:
info(1) = 0 for normal termination;
info(1) = -1 for lack of progress in either the predictor or corrector step;
info(1) = -2 if primal or dual step-lengths are too short;
info(1) = -3 if the primal or dual iterates lose positive definiteness;
info(1) = -4 if the Schur complement matrix becomes singular;
info(1) = -10 for incorrect input;
info(1) = 1 if there is an indication of primal infeasibility;
info(1) = 2 if there is an indication of dual infeasibility; and
info(1) = 3 if there is an indication of both primal and dual infeasibilities.

If info(1) is positive, the output variables X,y,Z have a different meaning: if info(1) = 1 or 3 then y,Z gives an indication of primal infeasibility: b y = 1 and y + Z is small, while if info(1) = 2 or 3 then X gives an indication of dual infeasibility: C X = -1 and X is small.

Global variables for parameters.
sdp.m and sdphlf.m use a number of global variables which are set up in the M-file startup.m. If desired, the user can change the values of these parameters. gam: step-length parameter. To use the default, set gam = 0; otherwise, set gam to the desired fixed value, say gam = 0.98.

predcorr: a 0-1 flag indicating whether to use the Mehrotra-type predictor-corrector. The default is 1.

expon: a vector specifying the lower bound for the exponent to be used in updating the centering parameter in the predictor-corrector algorithm, where

expon(1): for the AHO direction,
expon(2): for the HKM direction,
expon(3): for the NT direction, and
expon(4): for the GT direction.

The default is expon = [3 1 1 2].

steptol: the step-length threshold below which the iteration is terminated. The default is 1e-6.

gaptol: the required accuracy in the duality gap as a fraction of the value of the objective functions. The default is 1e-13.

maxit: maximum number of iterations allowed. The default is 50.

sw2PC_tol: the infeasibility measure threshold below which the predictor-corrector step is applied. The default is sw2PC_tol = Inf.

use_corrprim: a 0-1 flag indicating whether to correct for primal infeasibility. The default is 1 for sdp.m, but 0 for sdphlf.m.

printyes: a 0-1 flag indicating whether to display the result of each iteration. The default is 1.

One global parameter, vers, is not set in the M-file startup.m and has to be specified by the user. It takes the following values: vers: type of search direction to be used, where

vers = 1 corresponds to the AHO direction,
vers = 2 corresponds to the HKM direction,
vers = 3 corresponds to the NT direction, and
vers = 4 corresponds to the GT direction.

Cell array representation for problem data.

Our implementation SDPT3 exploits the block-diagonal structure of the given data, and C. Suppose the matrices and C are block-diagonal of the same structure. If the initial iterate is chosen to have the same block-diagonal structure, then this structure is preserved for all the subsequent iterates (X,Z). For reasons that will be explained later, if there are numerous small blocks each of dimension say less than 10, we group them together as a single sparse block-diagonal matrix instead of considering them as individual blocks. Suppose now that each of the matrices and C consists of L blocks of square matrices of dimensions . We can classify each of these blocks into one of the following three types:

1. a dense or sparse matrix of dimension greater than or equal to 10;
2. a sparse block-diagonal matrix consisting of numerous sub-blocks each of dimension less than 10;
3. a diagonal matrix.

For each SDP problem, the block-diagonal structure of and C is described by an cell array named blk where the content of each of its elements is given as follows. If the ith block of each and C is a dense or sparse matrix of dimension greater than or equal to 10, then

    blk{i,1} =  'nondiag'    blk{i,2} =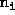  
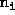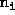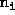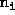    A{i,k}, C{i} = [  x   double] or [  x   sparse].

(It is possible for some 's to have a dense ith block and some to have a sparse ith block, and similarly the ith block of C can be either dense or sparse.) If the ith block of each and C is a sparse matrix consisting of numerous small sub-blocks, say t of them, of dimensions such that , then

    blk{i,1} =  'nondiag'    blk{i,2} = [          ]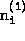 
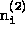
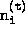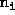    A{i,k}, C{i} = [  x 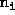  sparse].

If the ith block of each and C is a diagonal matrix, then

    blk{i,1} =  'diag'     blk{i,2} =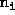   
    A{i,k}, C{i} = [  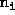x1 double].

As an example, suppose each of the 's and C has block structure as shown in Figure 1;

  
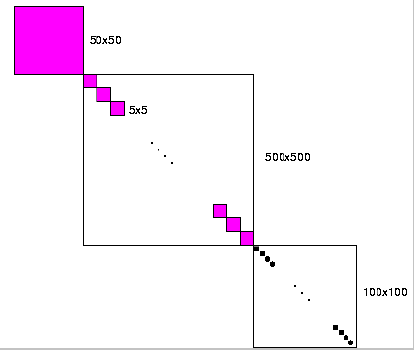
Figure 1: An example of a block-diagonal matrix.

then we have

    blk{1,1} =  'nondiag'   blk{1,2} =  50
    blk{2,1} =  'nondiag'   blk{2,2} =  [5 5  5] 
    blk{3,1} =  'diag'      blk{3,2} =  100

and the matrices and C are stored in cell arrays as

    A{1,k}, C{1} = [50x50 double]
    A{2,k}, C{2} = [500x500 sparse]  
    A{3,k}, C{3} = [100x1 double]

Notice that when the block is a diagonal matrix, only the diagonal elements are stored, and they are stored as a column vector.

Recall that when a block is a sparse block-diagonal matrix consisting of t sub-blocks of dimensions , we can actually view it as t individual blocks, in which case there will be t cell array elements associated with the t blocks rather than just one single cell array element originally associated with the sparse block-diagonal matrix. The reason for using the sparse matrix representation to handle the case when we have numerous small diagonal blocks is that it is less efficient for MATLAB to work with a large number of cell array elements compared to working with a single cell array element consisting of a large sparse block-diagonal matrix. Technically, no problem will arise if one chooses to store the small blocks individually instead of grouping them together as a sparse block-diagonal matrix.

We should also mention the function file ops.m used in our package. The purpose of this file is to facilitate arithmetic operations on the contents of any two cell arrays with constituents that are matrices of the same dimensions.

For the usage of MATLAB cell arrays, refer to [7].

Complex data.
Complex SDP data are allowed in our package. The user does not have to make any declaration even when the data is complex. Our codes will automatically detect this if it is the case.

Caveats.
The user should be aware that semidefinite programming is more complicated than linear programming. For example, it is possible that both primal and dual problems are feasible, but their optimal values are not equal. Also, either problem may be infeasible without there being a certificate of that fact (so-called weak infeasibility). In such cases, our software package is likely to terminate after some iterations with an indication of short step-length or lack of progress. Also, even if there is a certificate of infeasibility, our infeasible-interior-point methods may not find it. Our homogeneous self-dual methods may also fail to detect infeasibility, but they are practical variants of theoretical methods that are guaranteed to obtain certificates of infeasibility if such exist. In our very limited testing on strongly infeasible problems, most of our algorithms have been quite successful in detecting infeasibility.