Our algorithms can start with an infeasible starting point.
However, the performance of these algorithms is quite sensitive
to the choice of the initial iterate. As observed in [5],
it is desirable to choose an initial iterate that
at least has the same order of magnitude as an optimal solution
of the SDP.
Suppose the matrices ![]() and C
are block-diagonal of the same structure, each consisting of
L blocks of square matrices of dimensions
and C
are block-diagonal of the same structure, each consisting of
L blocks of square matrices of dimensions ![]() .
Let
.
Let ![]() and
and ![]() denote the ith block of
denote the ith block of
![]() and C, respectively.
If a feasible starting point is not known,
we recommend that the following initial iterate be used:
and C, respectively.
If a feasible starting point is not known,
we recommend that the following initial iterate be used:
where ![]() ,
,
![]() is the identity matrix of order
is the identity matrix of order ![]() , and
, and
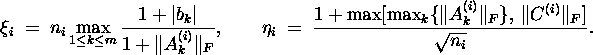
By multiplying the identity matrix ![]() by the factors
by the factors ![]() and
and ![]() for each i,
the initial iterate has a better chance of having the same
order of magnitude as an optimal solution of the SDP.
for each i,
the initial iterate has a better chance of having the same
order of magnitude as an optimal solution of the SDP.
The initial iterate
above is set by calling infeaspt.m, with initial line
function [X0,y0,Z0] = infeaspt(blk,A,C,b,options),
where options = 1 (default) corresponds to the
initial iterate just described; and options = 2 corresponds
to the choice where X0, Z0 are identity matrices
and y0 is a zero vector.