The homogeneous predictor-corrector algorithm

The Mehrotra-type predictor-corrector variant of the homogeneous path-following algorithm is as follows.

Remarks.

(a) The numerical instability of the Schur complement equation (28) arising from the homogeneous algorithms appears to be much more severe than that of the infeasible path-following algorithms as 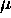decreases to zero. We overcome this difficulty by first setting 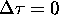and then computing 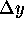in (28) when 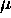is smaller than 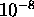. In essence, this amounts to switching to the infeasible path-following algorithms where the Schur complement equation (9) is numerically more stable.

(b) For the homogeneous algorithms, it seems not desirable to correct for the primal infeasibility so as keep the primal infeasibility below a certain small level once that level has been reached. The effect of such a correction can be quite erratic, in contrast to the case of the infeasible path-following algorithms.

(c) Once again, there are other termination criteria: lack of progress or short step-lengths. Here we do not test possible infeasibility in the way we did for our infeasible-interior-point algorithms, because we have a specific termination criterion ((b) in the descriptions above) to detect infeasibility.

(Remarks (a) and (b) are based on computational experience rather than our having any explanation at this time.)