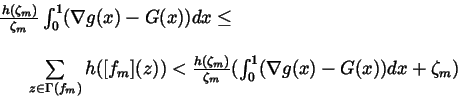Next: Another choice for and
Up: Free Energies for Structured
Previous: Limiting behavior of the
From the analysis in Subsection 2.4, it suffices to consider the case
 ,
and Proposition 2.1 reduces our task to veryfying: for
each
,
and Proposition 2.1 reduces our task to veryfying: for
each
 ,
there exists a sequence of simple
deformations satisfying
,
there exists a sequence of simple
deformations satisfying
 and
and
)=L\int\limits_0^1(\nabla g(x)-G(x))dx.
\end{displaymath}](img186.gif) |
(9) |
Our first step in constructing such a sequence is to consider the case
 for all
for all
 .
In this case,
.
In this case,
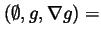
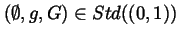 ,
and we may put
,
and we may put
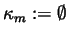 and fm:=g for every positive integer m. Thus,
and fm:=g for every positive integer m. Thus,
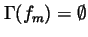 and
and
)=0=\int_0^1(\nabla
g(x)-G(x))\,dx$](img192.gif) for all m, so that (2.9) is evident.
for all m, so that (2.9) is evident.
The remaining case to consider is when there exists
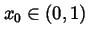 for which
for which
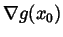
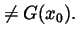 The continuity of
The continuity of 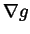 and of G and the
relations
and of G and the
relations
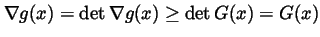 for all
for all
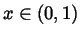 imply that
imply that
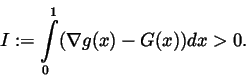 |
(10) |
By the definition
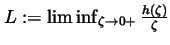 ,
we may choose
,
we may choose
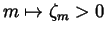 such that
such that
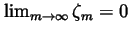 and
and
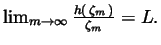 Moreover, we may assume that
Moreover, we may assume that
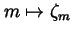 is strictly decreasing
and, because I>0, that
is strictly decreasing
and, because I>0, that
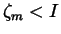 for all m. Let m now be
given, and note that, because the function
for all m. Let m now be
given, and note that, because the function 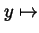
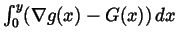 is continuous, we may choose a number
xq1
is continuous, we may choose a number
xq1 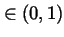 such that
such that
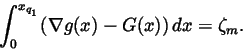 |
(11) |
For x in the interval
(0,xq1), put
 |
(12) |
and note that
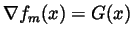 and
and
To define fm on
(xq1,1), we first consider the case
For
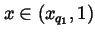 we define
we define
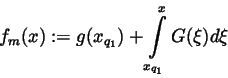 |
(13) |
and we note as above that
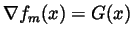 and
and
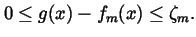 Relations (2.12) and (2.13) tell us that
Relations (2.12) and (2.13) tell us that
and it follows that
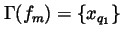 and
and
=\zeta
_m>0.$](img218.gif) Consequently,
Consequently,
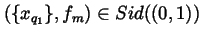 ,
the condition (ii)
in Proposition 2.2 is satisfied, and
,
the condition (ii)
in Proposition 2.2 is satisfied, and
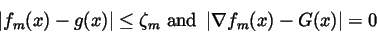 |
(14) |
for all

In the remaining case
we may choose xq2
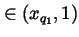 such that
such that
and for x in the interval
(xq1,xq2) we define fm(x) again
using the formula (2.13), so that the relations (2.14) are
satisfied for all
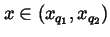 and
and
=\zeta _m>0$](img226.gif) .
If we now put
.
If we now put
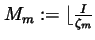 ,
i.e., the greatest integer
less than or equal to the number
,
i.e., the greatest integer
less than or equal to the number
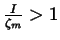 ,
then we may choose
for each
,
then we may choose
for each
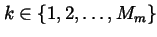 a point
a point
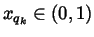 such that
such that
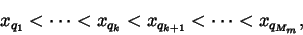 |
(15) |
and
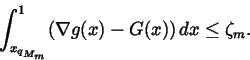 |
(17) |
We now define
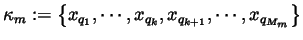 and, setting
xq0:=0 and
xqMm+1:=1,we put
and, setting
xq0:=0 and
xqMm+1:=1,we put
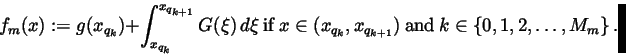 |
(18) |
This definition yields a simple deformation
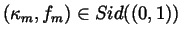 with
with
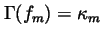 ,
,
=\zeta _m$](img240.gif) for all
for all
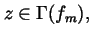 and satisfying (2.14) for all
and satisfying (2.14) for all
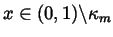 .
We now may write
.
We now may write
In other words, for all positive integers m,
and, letting
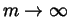 ,
we obtain the desired relation(2.9).
,
we obtain the desired relation(2.9).




Next: Another choice for and
Up: Free Energies for Structured
Previous: Limiting behavior of the
Nancy J Watson
1999-09-30
![]() ,
and Proposition 2.1 reduces our task to veryfying: for
each
,
and Proposition 2.1 reduces our task to veryfying: for
each
![]() ,
there exists a sequence of simple
deformations satisfying
,
there exists a sequence of simple
deformations satisfying
![]() and
and
![]() for all
for all
![]() .
In this case,
.
In this case,
![]()
![]() ,
and we may put
,
and we may put
![]() and fm:=g for every positive integer m. Thus,
and fm:=g for every positive integer m. Thus,
![]() and
and
)=0=\int_0^1(\nabla
g(x)-G(x))\,dx$](img192.gif) for all m, so that (2.9) is evident.
for all m, so that (2.9) is evident.
![]() for which
for which
![]()
![]() The continuity of
The continuity of ![]() and of G and the
relations
and of G and the
relations
![]() for all
for all
![]() imply that
imply that
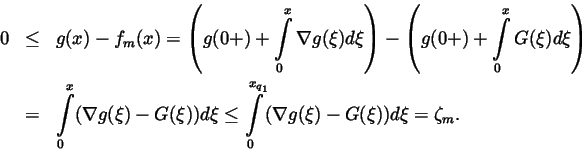
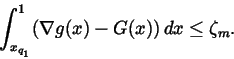
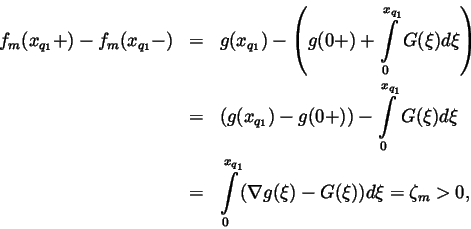
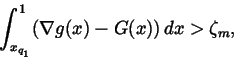
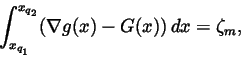
![]() with
with
![]() ,
,
![]() for all
for all
![]() and satisfying (2.14) for all
and satisfying (2.14) for all
![]() .
We now may write
.
We now may write
) &=&\sum\limits_{z\in...
...ta _m)}{\zeta _m},(\frac{I\,}{%
\zeta _m}+1)h(\zeta _m)\right) .
\end{eqnarray*}](img243.gif)