



Next: Proof of Proposition 2.2
Up: Free Energies for Structured
Previous: Limiting behavior of the
We begin by listing the points of
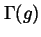 in increasing order
in increasing order
and we consider for each positive integer m as above and
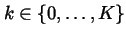 the pair
the pair
and the triple
It is easy to see that
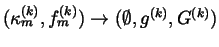 ,
that
,
that
and
).
\end{displaymath}](img162.gif) |
(5) |
Therefore, to find the behavior of the left hand side of (2.5) as
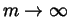 ,
it suffices to determine the behavior of
,
it suffices to determine the behavior of
)$](img163.gif) as
as
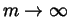 for each
for each
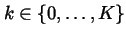 .
Thus, without loss
of generality, we may now replace
.
Thus, without loss
of generality, we may now replace
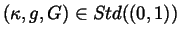 by
by
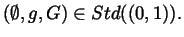
Proposition 2.1
Let
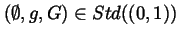
be given and let
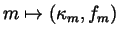
be a sequence of simple deformations such that
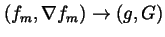
and, for all positive integers
m and
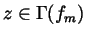
,
there holds
[
fm](
z)>0. It follows that
)\geq
L\int\limits_0^1(\nabla g(x)-G(x))dx
\end{displaymath}](img166.gif) |
(6) |
with
L the non-negative number defined in (
2.2).
Proof. Because
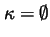 ,
the function g is
continuous, so that [g](z)=0 for all
,
the function g is
continuous, so that [g](z)=0 for all
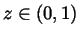 .
By the Trace Theorem
and the continuity of g, we may conclude that
.
By the Trace Theorem
and the continuity of g, we may conclude that
\,\mid \,z\in \Gamma (f_m)\right\} =0$](img169.gif) .
The definition
of ``lim inf'' and the assumed positivity of [fm(z)] tell us that, for
each
.
The definition
of ``lim inf'' and the assumed positivity of [fm(z)] tell us that, for
each
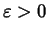 ,
we may choose a positive integer
,
we may choose a positive integer
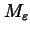 such that
such that
for all
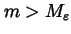 and
and
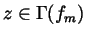 .
Multiplying both members
of this inequality by [fm](z) and summing over
.
Multiplying both members
of this inequality by [fm](z) and summing over
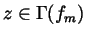 we
find
we
find
and this yields the desired conclusion.
The next result gives us full information about the limiting behavior of the
interfacial energy not associated with the jumps of g.
Proposition 2.2
For every
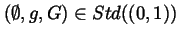
,
)\right) =L\int\limits_0^1(\nabla g(x)-G(x))dx
\end{displaymath}](img175.gif) |
(7) |
with
L the non-negative number defined in (
2.2) and with the
infimum taken over the sequences of simple deformations satisfying (i)
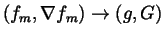
and (ii)
[
fm](
z)>0 for all positive
integers
m and for all
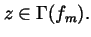
Before we prove this proposition, we discuss the important and immediate
conclusion that we may draw from it and the results in Subsections 2.2 and
2.3:
with again L the non-negative number defined in (2.2) and with
the infimum taken over the sequences of simple deformations satisfying (i)
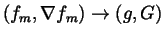 and (ii)
[fm](z)>0 for all positive
integers m and for all
and (ii)
[fm](z)>0 for all positive
integers m and for all
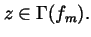 This result captures the
flavor of the conclusions obtained by Choksi & Fonseca [2]: (1) it
involves the double limit operation ``
This result captures the
flavor of the conclusions obtained by Choksi & Fonseca [2]: (1) it
involves the double limit operation ``
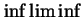 '' to yield a
quantity depending only upon (g,G) and not on a particular choice of
sequence satisfying (i) and (ii); (2) the bulk term
'' to yield a
quantity depending only upon (g,G) and not on a particular choice of
sequence satisfying (i) and (ii); (2) the bulk term
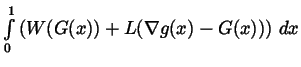 on the right-hand side of (2.8) contains two terms in the integrand: one comes from the bulk
energy density W and the other comes from the interfacial energy density <tex2htmlcommentmark>
h for simple deformations. Thus, the diffusion of disarrangements
occurring as m tends to infinity causes the interfacial energy for simple
deformations to contribute to the limiting bulk energy, while the persistent
disarrangements associated with
on the right-hand side of (2.8) contains two terms in the integrand: one comes from the bulk
energy density W and the other comes from the interfacial energy density <tex2htmlcommentmark>
h for simple deformations. Thus, the diffusion of disarrangements
occurring as m tends to infinity causes the interfacial energy for simple
deformations to contribute to the limiting bulk energy, while the persistent
disarrangements associated with
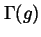 cause the initial interfacial
energy for simple deformations to contribute to the limiting interfacial
energy. If we followed Choksi & Fonseca one step further, we would define
cause the initial interfacial
energy for simple deformations to contribute to the limiting interfacial
energy. If we followed Choksi & Fonseca one step further, we would define
Instead, we give at the end of this lecture an alternative method for
calculating an energy for structured deformation that leads to terms in the
integral that can depend non-linearly on
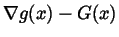 ,
the deformation
due to microdisarrangements.
,
the deformation
due to microdisarrangements.




Next: Proof of Proposition 2.2
Up: Free Energies for Structured
Previous: Limiting behavior of the
Nancy J Watson
1999-09-30
![]() in increasing order
in increasing order
)$](img163.gif) as
as
![]() ,
the function g is
continuous, so that [g](z)=0 for all
,
the function g is
continuous, so that [g](z)=0 for all
![]() .
By the Trace Theorem
and the continuity of g, we may conclude that
.
By the Trace Theorem
and the continuity of g, we may conclude that
![]() .
The definition
of ``lim inf'' and the assumed positivity of [fm(z)] tell us that, for
each
.
The definition
of ``lim inf'' and the assumed positivity of [fm(z)] tell us that, for
each
![]() ,
we may choose a positive integer
,
we may choose a positive integer
![]() such that
such that
)}{[f_m](z)}\geq (1-\varepsilon )L
\end{displaymath}](img172.gif)
) &\geq &(1-\varepsilo...
...
&=&(1-\varepsilon )L\,\int\limits_0^1\,(\nabla g(x)-G(x))\,dx,
\end{eqnarray*}](img174.gif)
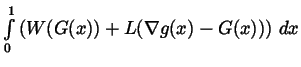 on the right-hand side of (2.8) contains two terms in the integrand: one comes from the bulk
energy density W and the other comes from the interfacial energy density <tex2htmlcommentmark>
h for simple deformations. Thus, the diffusion of disarrangements
occurring as m tends to infinity causes the interfacial energy for simple
deformations to contribute to the limiting bulk energy, while the persistent
disarrangements associated with
on the right-hand side of (2.8) contains two terms in the integrand: one comes from the bulk
energy density W and the other comes from the interfacial energy density <tex2htmlcommentmark>
h for simple deformations. Thus, the diffusion of disarrangements
occurring as m tends to infinity causes the interfacial energy for simple
deformations to contribute to the limiting bulk energy, while the persistent
disarrangements associated with
).
\end{displaymath}](img183.gif)