Next: Application to Shape Design:
Up: The Main Idea
Previous: Constructing The Preconditioner from
The previous section discussed the construction of preconditioners from
their symbol in case the design space was a space of functions defined,
for example, on the boundary of a domain. This is the infinite dimensional
design space.
In many applications one uses a fixed
finite dimensional representation of the design space, using a set of
prescribed shape functions. When the number of these functions is small
one can use acceleration techniques such as BFGS. When that number grows and the number of BFGS
steps required to solve the problem increases significantly, one may combine a preconditioner which is based
on the infinite dimensional analysis.
We consider two design spaces. The first, 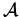 , is a space of functions
which is infinite dimensional and the second one,
, is a space of functions
which is infinite dimensional and the second one, 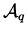 , is a subspace
of the first and is represented in terms of
, is a subspace
of the first and is represented in terms of 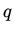 functions,
functions,
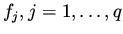 .
We also assume that the set
.
We also assume that the set
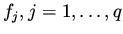 is orthonormal with respect to
the usual
is orthonormal with respect to
the usual 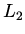 inner product on the boundary,
inner product on the boundary,
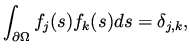 |
|
|
(27) |
where 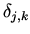 is the Kronecker delta.
Functions in
is the Kronecker delta.
Functions in 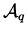 are linear combination of the form
are linear combination of the form
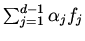 ,
and the space
,
and the space 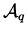 can be identified
can be identified 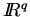 . We construct
a mapping
. We construct
a mapping 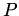 from
from 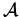 to
to 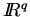 by,
by,
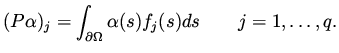 |
|
|
(28) |
Note that the transpose of the operator 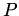 acts from the finite dimensional
space
acts from the finite dimensional
space 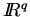 to
to 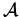 and is given by
and is given by
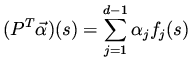 |
|
|
(29) |
where
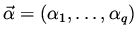 .
.
Now we come to the point of relating gradients calculated with respect to the
design space 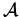 to those calculated with respect to
to those calculated with respect to 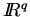 .
Let
.
Let
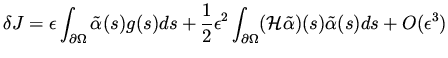 |
|
|
(30) |
be the variation of the functional corresponding to a change in the design
variables by
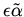 . The gradient with respect to
. The gradient with respect to 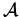 is certainly
is certainly 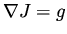 , and the Hessian is
, and the Hessian is 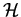 .
Now if the change in the design variables are done
in the subspace
.
Now if the change in the design variables are done
in the subspace 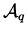 , we consider
, we consider
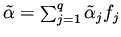 and then
a substitution into the above expression for
and then
a substitution into the above expression for 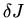 gives
gives
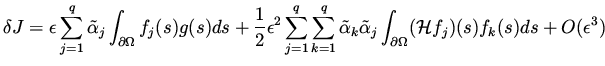 |
|
|
(31) |
and in that case
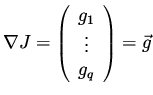 |
|
|
(32) |
where
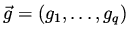 ,
,
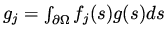 , and the Hessian
for the subspace,
, and the Hessian
for the subspace, 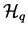 , is related to the full Hessian
, is related to the full Hessian 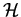 as
as
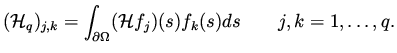 |
|
|
(33) |
Notice that for the finite dimensional design space we can write,
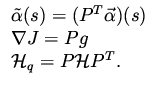 |
|
|
(34) |
These are the abstract formulas for the discrete quantities for the
subspace as a function of the same quantities on the infinite dimensional
space.
A preconditioner for the finite dimensional design can be obtained by constructing
first the infinite dimensional preconditioner and then using the above formula
to get
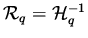 .
The preconditioned iteration is
.
The preconditioned iteration is
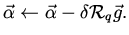 |
|
|
(35) |
Example Consider the case
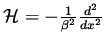 which appeared in one of the previous lectures.
The finite dimensional preconditioner is constructed from the inverse of
the finite dimensional Hessian
which appeared in one of the previous lectures.
The finite dimensional preconditioner is constructed from the inverse of
the finite dimensional Hessian
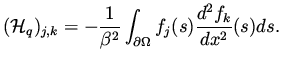 |
|
|
(36) |



Next: Application to Shape Design:
Up: The Main Idea
Previous: Constructing The Preconditioner from
Shlomo Ta'asan
2001-08-22
![]() , is a space of functions
which is infinite dimensional and the second one,
, is a space of functions
which is infinite dimensional and the second one, ![]() , is a subspace
of the first and is represented in terms of
, is a subspace
of the first and is represented in terms of ![]() functions,
functions,
![]() .
We also assume that the set
.
We also assume that the set
![]() is orthonormal with respect to
the usual
is orthonormal with respect to
the usual ![]() inner product on the boundary,
inner product on the boundary,
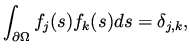
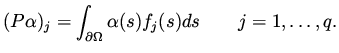
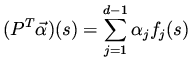
![]() to those calculated with respect to
to those calculated with respect to ![]() .
Let
.
Let
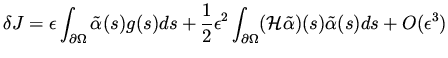
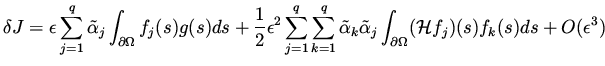
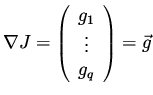
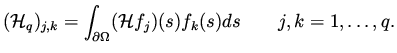
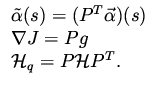
![]() .
The preconditioned iteration is
.
The preconditioned iteration is
![]() which appeared in one of the previous lectures.
The finite dimensional preconditioner is constructed from the inverse of
the finite dimensional Hessian
which appeared in one of the previous lectures.
The finite dimensional preconditioner is constructed from the inverse of
the finite dimensional Hessian