


Next: Constructing The Preconditioner from
Up: Infinite Dimensional Preconditioners for
Previous: Introduction
Gradient based methods can be viewed as relaxation methods for the equation
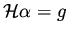 |
|
|
(1) |
where 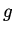 is the gradient and
is the gradient and 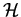 is the Hessian of the functional
considered. For example, a Jacobi relaxation for equation (1) has the form
is the Hessian of the functional
considered. For example, a Jacobi relaxation for equation (1) has the form
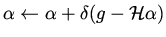 |
|
|
(2) |
which is essentially the steepest descent method for minimizing
the cost functional.
The observation that the convergence rate for gradient descent methods is
governed by
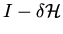 suggests that effective
Preconditioners can be constructed using the behavior of
the symbol of the Hessian
suggests that effective
Preconditioners can be constructed using the behavior of
the symbol of the Hessian
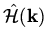 , for large
, for large
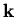 . The idea is simple. Assume that
. The idea is simple. Assume that
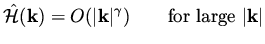 |
|
|
(3) |
and let 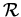 be an operator whose symbol
satisfies
be an operator whose symbol
satisfies
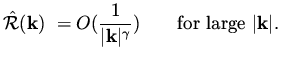 |
|
|
(4) |
The behavior of the preconditioned method
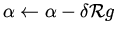 |
|
|
(5) |
is determined by
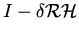 |
|
|
(6) |
whose symbol
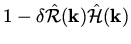 |
|
|
(7) |
approaches a constant for large 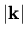 .
A proper choice of
.
A proper choice of 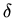 leads to a convergence
rate which is independent of the dimensionality of the design space.
This is not the case if the symbol of the iteration operator has some
dependence on
leads to a convergence
rate which is independent of the dimensionality of the design space.
This is not the case if the symbol of the iteration operator has some
dependence on 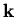 .
.
It is desired not to change the behavior of the low frequencies by
the use of the preconditioner, since the analysis we do
for the Hessian does not hold in the limit
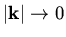 .
That is, we would like the symbol of the preconditioner to satisfy also,
.
That is, we would like the symbol of the preconditioner to satisfy also,
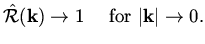 |
|
|
(8) |
Subsections



Next: Constructing The Preconditioner from
Up: Infinite Dimensional Preconditioners for
Previous: Introduction
Shlomo Ta'asan
2001-08-22
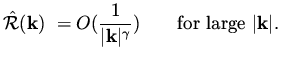
![]() .
That is, we would like the symbol of the preconditioner to satisfy also,
.
That is, we would like the symbol of the preconditioner to satisfy also,