


Next: Problems Classification
Up: Fourier Analysis For Optimization
Previous: Fourier Analysis For Optimization
In order to get a quantitative description of the level curves of the
cost functional and to be able to determine the structure of the functional
near the minimum, a Fourier analysis of the Hessian of the functional is
carried out. In many problems of engineering interest the design variable
are associated with boundary quantities and the gradient of the cost
function as well as the Hessian are quantities defined on part of the
boundary as well.
We have seen in lecture 1 that the eigenvalue distribution of the Hessian plays an important role in convergence rates for the optimization problem.
Moreover, the asymptotic behavior of the large eigenvalues of the
Hessian is tightly related to
the symbol of the Hessian. Its computation is therefore of practical importance.
In the next example
we calculate the symbol of the Hessian for a control problem related to a shape design
problem. We identify in this case the Hessian as a differential operator
acting on functions defined on the boundary of the domain.
Example V Consider the following minimization problem,
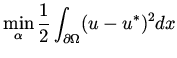 |
|
|
(36) |
subject to
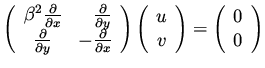 |
|
|
(37) |
with the boundary condition
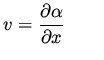 |
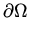 |
|
(38) |
where
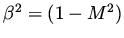 and
and
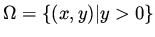 .
We introduce adjoint variables (Lagrange multipliers)
.
We introduce adjoint variables (Lagrange multipliers)
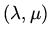 which can be shown to satisfy
which can be shown to satisfy
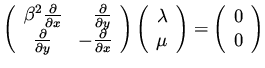 |
|
|
(39) |
with the boundary condition
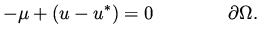 |
|
|
(40) |
At the minimum the following equation has to be satisfied
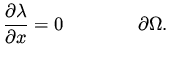 |
|
|
(41) |
The left hand side of this equation is the gradient of the functional subject to
the PDE, and its behavior in the
vicinity of the minimum needs to be analyzed.
In order to do that we examine the perturbation in the solution as a result
of a perturbation in the design function 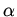 . The linearity of the
interior equation
implies that the perturbation variables
. The linearity of the
interior equation
implies that the perturbation variables
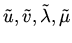 satisfy the same equations as
satisfy the same equations as
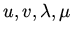 in
the interior of the domain, and the boundary conditions for them are
in
the interior of the domain, and the boundary conditions for them are
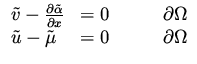 |
|
|
(42) |
and the change in the gradient is given by
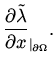 |
|
|
(43) |
The analysis continues by assuming 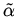 to be a Fourier component,
that is,
to be a Fourier component,
that is,
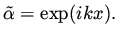 |
|
|
(44) |
From the boundary condition we get
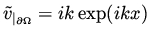 and using the interior equations
(37) for
and using the interior equations
(37) for
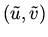 we conclude that
we conclude that
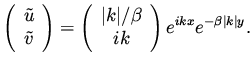 |
|
|
(45) |
Using the boundary conditions for 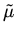 we get
we get
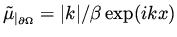 and from the interior equations (39) for
and from the interior equations (39) for
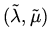 it is easy to see that
it is easy to see that
Combining these results we obtain that the change in the gradient,
corresponding to a change in the design variable by
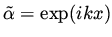 is
is
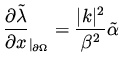 |
|
|
(46) |
Thus, the symbol of the Hessian
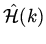 is given
by
is given
by
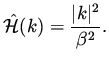 |
|
|
(47) |
This symbol correspond to the differential operator
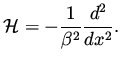 |
|
|
(48) |
A General Remark:
This analysis was performed on problems with constant coefficients, however, it
is not limited to such cases. It
can be applied to non-constant coefficients and
nonlinear problems in general domains. In such cases one linearizes the problem
(if it is nonlinear)
and freezes coefficients at a point 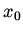 in the domain. A constant coefficient
problem is obtained which describes the behavior of the problem in a small
vicinity of that point. The validity
of the resulting Fourier analysis for that problem is then restricted to a small
vicinity. Usually, all expressions in the analysis will depend on the
frozen coefficients and analyzing one point in the domain is enough to
obtain the desired information about all points.
The rigorous justification of
this process is beyond the scope of our discussion here.
in the domain. A constant coefficient
problem is obtained which describes the behavior of the problem in a small
vicinity of that point. The validity
of the resulting Fourier analysis for that problem is then restricted to a small
vicinity. Usually, all expressions in the analysis will depend on the
frozen coefficients and analyzing one point in the domain is enough to
obtain the desired information about all points.
The rigorous justification of
this process is beyond the scope of our discussion here.
When considering the problem in a general domain one perform the analysis
at a boundary point by transforming the vicinity of that point into 'half-space'
and applying there the analysis presented above. Thus, smooth boundaries can
be treated. This analysis is local and hence is relevant for high frequencies
only. Low frequencies are affected by the shape of the boundary and cannot
be analyzed using local techniques. However, in spite of this limitation,
it is still a very useful tool for quantitative results regarding our problems.



Next: Problems Classification
Up: Fourier Analysis For Optimization
Previous: Fourier Analysis For Optimization
Shlomo Ta'asan
2001-08-22
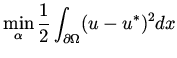
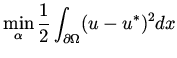
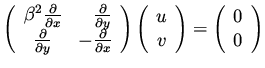
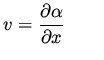
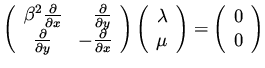
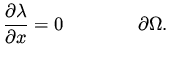
![]() . The linearity of the
interior equation
implies that the perturbation variables
. The linearity of the
interior equation
implies that the perturbation variables
![]() satisfy the same equations as
satisfy the same equations as
![]() in
the interior of the domain, and the boundary conditions for them are
in
the interior of the domain, and the boundary conditions for them are
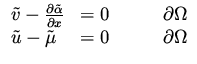
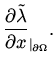
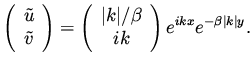
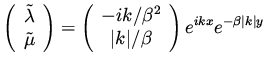
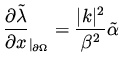
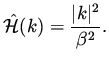
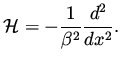
![]() in the domain. A constant coefficient
problem is obtained which describes the behavior of the problem in a small
vicinity of that point. The validity
of the resulting Fourier analysis for that problem is then restricted to a small
vicinity. Usually, all expressions in the analysis will depend on the
frozen coefficients and analyzing one point in the domain is enough to
obtain the desired information about all points.
The rigorous justification of
this process is beyond the scope of our discussion here.
in the domain. A constant coefficient
problem is obtained which describes the behavior of the problem in a small
vicinity of that point. The validity
of the resulting Fourier analysis for that problem is then restricted to a small
vicinity. Usually, all expressions in the analysis will depend on the
frozen coefficients and analyzing one point in the domain is enough to
obtain the desired information about all points.
The rigorous justification of
this process is beyond the scope of our discussion here.