


Next: The Symbol of The
Up: Theoretical Tools for Problem
Previous: The Symbol of an
The above analysis using Fourier decomposition can also serve for the
analysis of optimization problems.
Of probably the main concern for us is to define optimization problems
for our engineering tasks, that will be mathematically "good", or well-posed
in mathematical terminology.
We would like the problem to have a solution (existence), that the solution
will be unique (uniqueness) and that the solution will depend in a continuous way on
other parameters in the problem (continuous dependence).
We will see that these properties of the problem, at least when considering
the high frequency range, can be easily analyzed.
The usual rigorous mathematical techniques for these question are very
complex and may not be of a practical engineering use. Moreover, some
important details which are of engineering importance
are not present in the rigorous analysis, while they are present
in the formal Fourier techniques.
The characterization of the minimizer for an optimization
problem gives
the equation
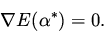 |
(33) |
This is in general a nonlinear equation for the unknown 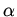 . Now lets
say that we have an approximate solution
. Now lets
say that we have an approximate solution 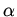 and we are seeking the
correction
and we are seeking the
correction 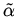 such that
such that
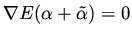 .
Using a Taylor expansion we see that
.
Using a Taylor expansion we see that 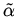 satisfies
approximately the equation
satisfies
approximately the equation
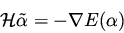 |
(34) |
where 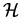 is the Hessian of the functional.
is the Hessian of the functional.
If the design variable 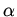 can be decomposed in a Fourier series
then important information can be obtain about the problem using Fourier analysis.
can be decomposed in a Fourier series
then important information can be obtain about the problem using Fourier analysis.
The symbol of the Hessian,
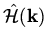 contains all
of the necessary information for analyzing and designing optimization
procedures.
Notice that, at the vicinity of the minimum,
the gradient of the functional,
contains all
of the necessary information for analyzing and designing optimization
procedures.
Notice that, at the vicinity of the minimum,
the gradient of the functional, 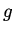 , is linearly related to the error.
In the Fourier space the relation is given by
, is linearly related to the error.
In the Fourier space the relation is given by
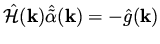 |
|
|
(35) |
where
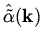 and
and
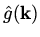 are the Fourier
transforms of
are the Fourier
transforms of
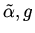 , respectively.
, respectively.
Subsections



Next: The Symbol of The
Up: Theoretical Tools for Problem
Previous: The Symbol of an
Shlomo Ta'asan
2001-08-22
![]() can be decomposed in a Fourier series
then important information can be obtain about the problem using Fourier analysis.
can be decomposed in a Fourier series
then important information can be obtain about the problem using Fourier analysis.
![]() contains all
of the necessary information for analyzing and designing optimization
procedures.
Notice that, at the vicinity of the minimum,
the gradient of the functional,
contains all
of the necessary information for analyzing and designing optimization
procedures.
Notice that, at the vicinity of the minimum,
the gradient of the functional, ![]() , is linearly related to the error.
In the Fourier space the relation is given by
, is linearly related to the error.
In the Fourier space the relation is given by