Frieze, Gionis, Tsourakakis
Tutorials
Tutorials
Algorithmic techniques for modeling and mining large graphs (AMAzING)
KDD 2013 , ECML PKDD 2013

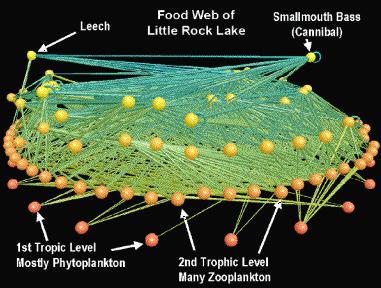
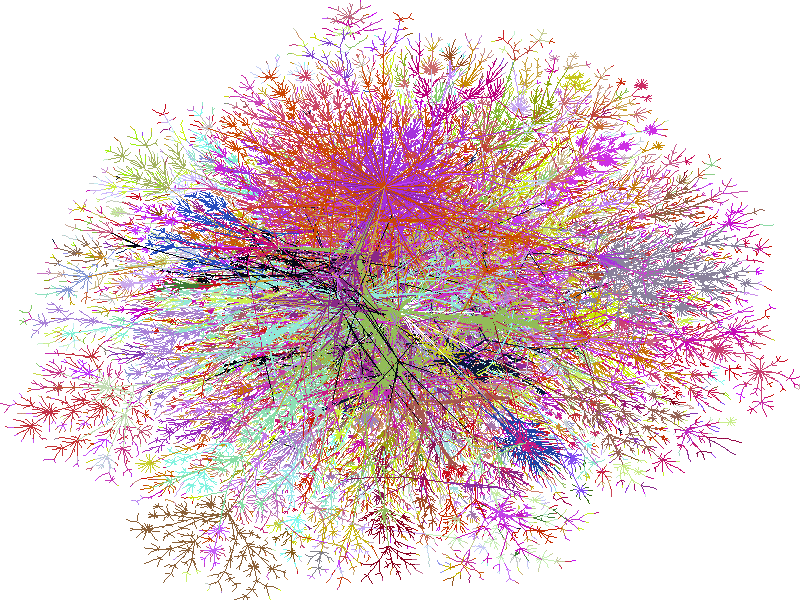
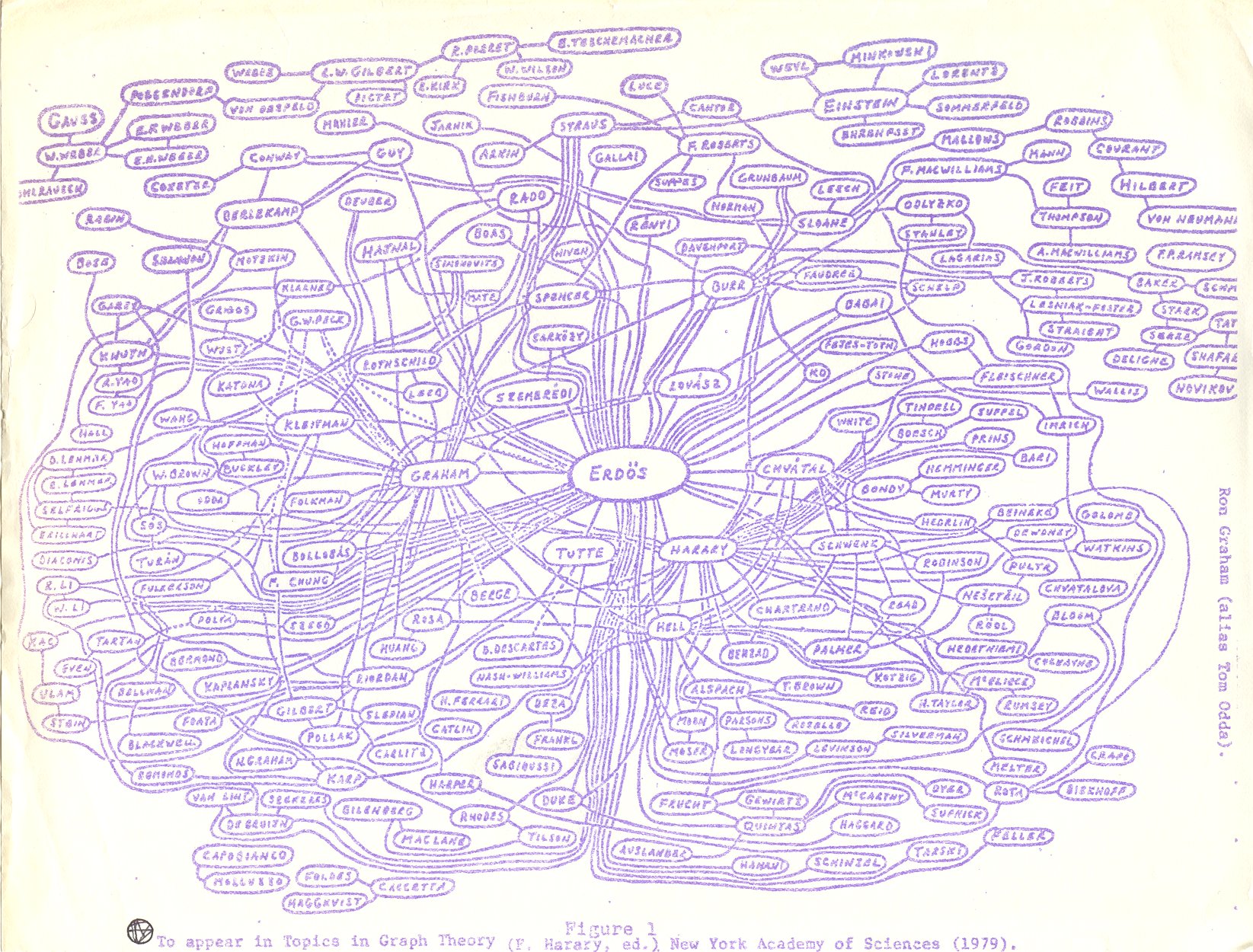
Slides
Download
Abstract
Network science has emerged over the last years as an interdisciplinary area spanning traditional domains including mathematics, computer science, sociology, biology and economics. Since complexity in social, biological and economical systems, and more generally in complex systems, arises through pairwise interactions there exists a surging interest in understanding networks.In this tutorial, we will provide an in-depth presentation of the most popular random-graph models used for modeling real-world networks. We will then discuss efficient algorithmic techniques for mining large graphs, with an emphasis on the problems of extracting graph sparsifiers, partitioning graphs into densely connected components, and finding dense subgraphs. We will motivate the problems, we will discuss algorithms to solve them and we will present real-world applications.
Our aim is to survey important results in the areas of modeling and mining large graphs, to uncover the intuition behind the key ideas, and to present future research directions.
Who Should Attend
The tutorial presents both classic and cutting-edge research topics on networks. We aim to go into depth for the following topics: random graphs, graph sparsifiers, graph partitioning, finding dense subgraphs and their applications. The tutorial will combine a blend of computer science rigor and real-world applications. It should be of theoretical and practical interest to the graph analysis community and a large part of the data mining community as well.Prerequisites
Computer science background (B.Sc or equivalent); familiarity with undergraduate level concepts covered in probability and algorithm classes.Tutorial Outline
- Part 0: Introduction
- Networks in our lives: where and how do networks appear?
- Part 1: Modelling Real World Networks
- What is a random graph?
- Erdös - Rényi random graphs
- Special properties of real-world networks
- Power law degree distribution
- Six Degrees, Small Worlds
- Clustering coefficients
- Eigenvalue power laws
- Triangle power laws
- Communities
- Assortative mixing
- Densification (time evolving networks)
- Models of real-world networks
- Barabasi-Albert/Bollobás-Riordan model
- Preferential attachment with fitness
- Cooper-Frieze model
- Geometric preferential attachment
- Affiliation networks
- Random Apollonian networks
- Kronecker graphs
- Chung-Lu model
- Evolving Copying model
- CHKNS model
- Watts-Strogatz model
- Case studies
- Search-engine bias
- Robustness and vulnerability of real-world networks
- Part 2: Algorithm Design for Large-Scale Networks
- Graph Sparsifiers
- Triangles Sparsifiers
- Cut Sparsifiers
- Spectral Sparsifiers
- Graph Partitioning
- Modularity and community detection
- Spectral partitioning, Cheeger's inequality
- Semidefinite programming (SDP) for graph partitioning
- Local algorithms
- Nibble algorithm of Spielman-Teng
- Evolving Sets (EvoCut)
- PageRank and graph partitioning
- Balanced graph partitioning
- Andreev-Räcke
- SDP
- Well-working Practices
- Label propagation
- METIS (offline)
- Stanton-Kliot (dynamic graphs)
- Fennel (dynamic graphs)
- Dense subgraphs
- Densest subgraph
- Exact algorithms
- Fast approximation algorithms
- Maximal cliques
- k-cores
- Quasi-cliques
- Part 3: Applications
- Spectral sparsification for efficient machine learning (quadratic minimization, LASSO type problems)
- Partitioning dynamic massive graphs for efficient solving of a wide range of computational tasks
- Clustering users in large scale e-mail services
- Dense subgraph applications in social network analysis and biology
- Part 4: Conclusion
- Suggesting additional material
- Research directions
Related Tutorials
- Graph Mining Techniques and Their Applications Sharma Chakravarthy EDBT 2006
- Data Mining for Social Network Analysis, Jaideep Srivastava, Nishith Pathak and Sandeep Mane, ICDM 2006
- Mining Large Graphs: Laws and Tools, C. Faloutsos, J. Leskovec, ECML-PKDD, 2007
- Mathematical Models of the World Wide Web, Alan Frieze, MAA-AMS meeting 2005
- Large Graph-Mining: Power Tools and a Practitioner's Guide, C. Faloutsos, G.L. Miller, C.E. Tsourakakis, KDD 2009
- Algorithms for mining large graphs, Aristides Gionis, Summer School on Massive Data Mining, IT University of Copenhagen, August 2012
References (with links)
Part 1: Properties of Real-world Networks
- On power-law relationships of the Internet topology, M. Faloutsos, P. Faloutsos, C. Faloutsos
- Complex networks: Structure and dynamics S. Boccaletti, V. Latora, Y. Moreno, M. Chavez, D. Hwang
- On the eigenvalue power law, M. Mihail, C. Papadimitriou
- Assortative mixing in networks, M. E. J. Newman
- Fast Counting of Triangles in Large Real Networks: Algorithms and Laws, C. Tsourakakis
- Graph Evolution: Densification and Shrinking Diameters, J. Leskovec, J. Kleinberg, C. Faloutsos
Part 1: Random Graphs
- Random graphs as models of networks , M. E.J. Newman
- Power-law distributions in empirical data, A. Clauset, C. Shalizi, M. E. J. Newman
- Emergence of scaling in random networks, L. Barabási, R. Albert
- The degree sequence of a scale-free random graph process,B. Bollobás, O. Riordan, J. Spencer, G. Tusnády:
- First to Market is not Everything: an Analysis of Preferential Attachment with Fitness, Christian Borgs, Jennifer Chayes, Constantinos Daskalakis, Sebastien Roch
- A General Model of Web Graphs, C. Cooper, A. Frieze
- A Geometric Preferential Attachment Model of Networks , A.Flaxman, A. Frieze, J.Vera
- Affiliation Networks, S. Lattanzi, D. Sivakumar
- On Certain Properties of Random Apollonian Networks, A. Frieze, C. Tsourakakis
- Kronecker Graphs: An Approach to Modeling Networks, Jure Leskovec, Deepayan Chakrabarti, Jon Kleinberg, Christos Faloutsos, Zoubin Ghahramani
- A random graph model for massive graphs, W. Aiello, F. Chung, L. Lu
- The similarity between stochastic Kronecker and Chung-Lu graph models , A. Pinar, C. Seshadhri, T. Kolda
- Moment based estimation of stochastic Kronecker graph parameters, D. Gleich, A. Owen
- Stochastic models for the web graph, R. Kumar, P. Raghavan, S. Rajagopalan, D. Sivakumar, A. Tomkins, E. Upfal
- Are randomly grown graphs really random?, D. S. Callaway, J. E. Hopcroft, J. M. Kleinberg, M. E. J. Newman, and S. H. Strogatz
- Heuristically optimized trade-offs: A new paradigm for power laws in the Internet, A. Fabrikant, E. Koutsoupias, C. Papadimitriou
- Estimating and Understanding Exponential Random Graph Models, S. Chatterjee, P. Diaconis
- Random graphs as models of networks , M. E.J. Newman
- Collective dynamics of 'small-world' networks, D.J. Watts, S.H. Strogatz
- Protean Graphs, T. Luczak, P. Pralat
- Crawling on web graphs, C. Cooper, A. Frieze
- Suppressing cascades of load in interdependent networks , Charles D. Brummitt, Raissa M. D’Souza, and E. A. Leicht
Part 2: Graph Sparsifiers
- Triangle Sparsifiers, C. E. Tsourakakis. M. N. Kolountzakis, G. L. Miller
- Randomized Approximation Schemes for Cuts and Flows in Capacitated Graphs, A. Benczúr, D. Karger
- Spectral Sparsification of Graphs, D. A. Spielman and S.-H. Teng.
- Graph sparsification by effective resistances, D. A. Spielman and N. Srivastava
Part 2: Dense Subgraphs
- Greedy approximation algorithms for finding dense components in a graph, M. Charikar
- Finding a maximum density subgraph, A. V. Goldberg
- A local algorithm for finding dense subgraphs, R. Andersen
- A fast parametric maximum flow algorithm and applications , G. Gallo, M.D. Grigoriadis, R.E. Tarjan
- Greedily finding a dense subgraph, Y. Asahiro, K. Iwama, H. Tamaki, T. Tokuyama
- Approximation algorithms for maximization problems arising in graph partitioning,U. Feige, M. Landberg
- On Finding Dense Subgraphs, S. Khuller, B. Saha
- Dense Subgraph Extraction with Application to Community Detection, Jie Chen, Yousef Saad
- Listing All Maximal Cliques in Large Sparse Real-World Graphs, D. Eppstein, D. Strash
- k-core organization of complex networks, S.N. Dorogovtsev, J.F.F. Goltsev, J.F. Mendes
- Massive quasi-clique detection, J. Abello, M. Resende, S. Sudarsky
Part 2: Graph Partitioning
- Community detection in graphs, Santo Fortunato
- Modularity and community structure in networks , M. E. J. Newman
- Modularity-Maximizing Graph Communities via Mathematical Programming, G. Agarwal, D. Kempe
- On modularity clustering , U. Brandes, D. Delling, M. Gaertler, R. Görke, M. Hoefer, Z. Nikoloski, and D. Wagner
- Resolution limit in community detection, S. Fortunato, M. Barthélemy
- Eigenvalues and expanders, N. Alon
- Fast Approximation Algorithms for Graph Partitioning using Spectral and Semidefinite-Programming Techniques, Lorenzo Orrechia
- Nearly-linear time algorithms for graph partitioning, graph sparsification, and solving linear systems, Daniel A. Spielman and S.-H. Teng.
- Community structure in large networks: Natural cluster sizes and the absence of large well-defined clusters, J. Leskovec, K.J. Lang, A. Dasgupta, and M.W. Mahoney
- Finding Sparse Cuts Locally Using Evolving Sets, R. Andersen, Y. Peres
- Local Graph Partitioning using PageRank Vectors, R. Andersen, F. Chung, K. Lang
- Partitioning Graphs into Balanced Components , Robert Krauthgamer, Joseph (Seffi) Naor, Roy Schwartz
- Balanced Graph Partitioning , Konstantin Andreev, Harald Räcke
- Fennel: Streaming Graph Partitioning for Massive Scale Graphs, Charalampos E. Tsourakakis, Christos Gkantsidis, Bozidar Radunovic, Milan Vojnovic
- Streaming Graph Partitioning for Large Distributed Graphs, Isabelle Stanton, Gabriel Kliot
- Balanced label propagation for partitioning massive graphs, Johan Ugander, Lars Backstrom
Part 3: Applications
- Runtime guarantees for regression problems, Hui Han Chin, Aleksander Madry, Gary L. Miller, Richard Peng
- Fast approximation of matrix coherence and statistical leverage, Petros Drineas, Malik Magdon-Ismail, Michael W. Mahoney, and David P. Woodruff
- Hermes: clustering users in large-scale e-mail services, Thomas Karagiannis, Christos Gkantsidis, Dushyanth Narayanan, Antony I. T. Rowstron
- The community-search problem and how to plan a successful cocktail party, Mauro Sozio, Aristides Gionis
- Discovering large dense subgraphs in massive graphs, D. Gibson, R. Kumar, A. Tomkins
- Trawling the Web for emerging cyber-communities, R. Kumar, P. Raghavan, S. Rajagopalan, and A. Tomkins.
- Extraction and Classification of Dense Communities in the Web, Y. Dourisboure, F. Geraci, M. Pellegrini
- A high-compression indexing scheme for reachability query, R. Jin, Y. Xiang, N. Ruan, D. Fuhry
- k-core decomposition: a tool for the visualization of large scale networks, J.I. Alvarez-Hamelin, L. Dall'Asta, A. Barrat, A. Vespignani
- MotifCut: regulatory motifs finding with maximum density subgraphs, E. Fratkin, BT. Naughton, DL. Brutlag, S. Batzoglou
Instructors
| Alan Frieze |  | Aristides Gionis |  |
Charalampos Tsourakakis |  |
Dr. Alan Frieze is a professor in the Department of Mathematical Sciences at Carnegie Mellon University, Pittsburgh, United States. He graduated from the University of Oxford in 1966, and obtained his Ph.D. from the University of London in 1975. His research interests lie in combinatorics, discrete optimization and theoretical computer science. In 1991, Dr. Frieze received the Fulkerson Prize in Discrete Mathematics awarded by the American Mathematical Society and the Mathematical Programming Society. In 1997 he was a Guggenheim Fellow In 2000, he received the IBM Faculty Partnership Award. In 2006 he jointly received (with Michael Krivelevich) the Professor Pazy Memorial Research Award from the United States-Israel Binational Science Foundation. In 2011 he was selected as a SIAM Fellow. In 2012 he was selected as an AMS fellow.
Dr. Aristides Gionis is an associate professor in the Department of Information and Computer Science, in Aalto University, Finland. Previously he has been a senior research scientist in Yahoo! Research. He received his Ph.D. from the Computer Science department of Stanford University in 2003. He is currently serving as an associate editor in the Transactions of Knowledge and Data Engineering (TKDE). He has served in the PC of numerous premium conferences, including being the PC co-chair for WSDM 2013 and ECML PKDD 2010. His research interests include data mining, web mining, and algorithmic data analysis.
Dr. Charalampos Tsourakakis is an Aalto Science Fellow. He received his Ph.D. in Algorithms, Combinatorics and Optimization at Carnegie Mellon University. He holds a Diploma in Electrical and Diploma Engineering from the National Technical University of Athens and a Master of Science from the Machine Learning Department at Carnegie Mellon University. His research interests include algorithm design, random graphs and data mining.