



Next: Limiting behavior of the
Up: Free Energies for Structured
Previous: Free energy for simple
Let
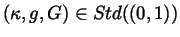 and
and
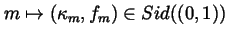 be given such that
be given such that
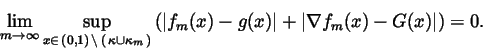 |
(3) |
In particular, we follow Choksi & Fonseca [2] in not requiring here
that
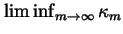
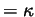 .
To distinguish this
weaker convergence (2.3), we write here
.
To distinguish this
weaker convergence (2.3), we write here
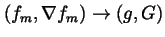 in place of the notation
in place of the notation
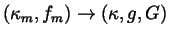 used in Part One for the convergence that includes the
requirement
used in Part One for the convergence that includes the
requirement
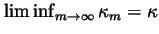 .
From the
definition of Std, we may choose positive constants
.
From the
definition of Std, we may choose positive constants
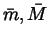 such
that
such
that
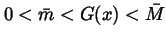 for all
for all
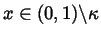 .
Because
.
Because
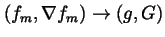 ,
we may choose a positive
integer N such that
,
we may choose a positive
integer N such that
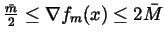 for
all
for
all
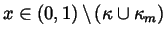 and for all m>N.
Since W is continuous, its restriction
and for all m>N.
Since W is continuous, its restriction
![$W\mid _{[\frac{\bar{m}}2,2\bar{M}%
]}\,$](img137.gif) is uniformly continuous, and we conclude that
is uniformly continuous, and we conclude that
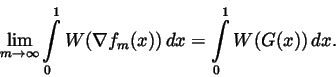 |
(4) |
Thus, the bulk energies for the approximating simple deformations
form a convergent sequence whose limit is independent of the choice of
sequence
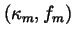
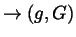 ;
in particular, the
limiting bulk energy depends only upon G, the deformation without
disarrangements.
;
in particular, the
limiting bulk energy depends only upon G, the deformation without
disarrangements.




Next: Limiting behavior of the
Up: Free Energies for Structured
Previous: Free energy for simple
Nancy J Watson
1999-09-30
![]() and
and
![]() be given such that
be given such that