REU: Geometry and Topology in a Discrete Setting
Research director: Prof. Florian Frick (Carnegie Mellon University)Numerous problems across mathematics may be "geometrized." This means that for a given problem one can consider the space of all potential solutions, which is a geometric object, and then use geometric and topological reasoning to find an actual solution in this space. In this research experience for undergraduates we will learn this way of thinking about mathematics and use it for several research problems. Some of these projects are geometric or topological themselves, while others are more combinatorial or analytic, depending on participants preferences.
Florian has advised more than 40 undergraduates on research projects over the last eight years. See some past projects below to get an impression. Prior knowledge of geometry and topology is not required. Participants should be passionate about learning a great deal of mathematics at the confluence of geometry, topology, and combinatorics.
The program will be integrated into the Mellon College of Science Summer Scholars Program. The program features a series of math talks, workshops about graduate school applications, CV and abstract writing exercises, presentation practice, and social activities.
When? May 28, 2024 − July 9, 2024 (6 weeks)
Where? Carnegie Mellon University, Pittsburgh, PA
Support: This REU is NSF-funded. US citizens and permanent residents are eligible to receive a stipend of $760 per week and fully paid on-campus housing. Domestic travel to and from the REU site will be reimbursed. Students not eligible for NSF-funding and students with support from their home institution may be accepted, depending on availability.
How to apply? Submit your application through MathPrograms.org. Your application should include current transcripts (unofficial transcripts are accepted), a personal statement of at most 1-2 pages (for example, about your motivation to participate in this program), a brief CV, and two letters of recommendation.
Questions? Reach out to Florian at frick@cmu.edu
Past REU projects
 |
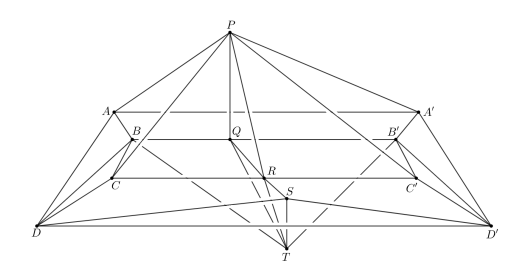
Splitting loops and necklaces: Variants of the square peg problem In 1972 Hugo Hadwiger conjectured that any closed curve in 3-space inscribes a parallelogram. In this project, we prove this conjecture by exhibiting a connection to measure partition problems in the unit interval − more precisely a variant of the Hobby-Rice theorem in functional analysis. This variant reduces to the Borsuk-Ulam theorem in topology. |
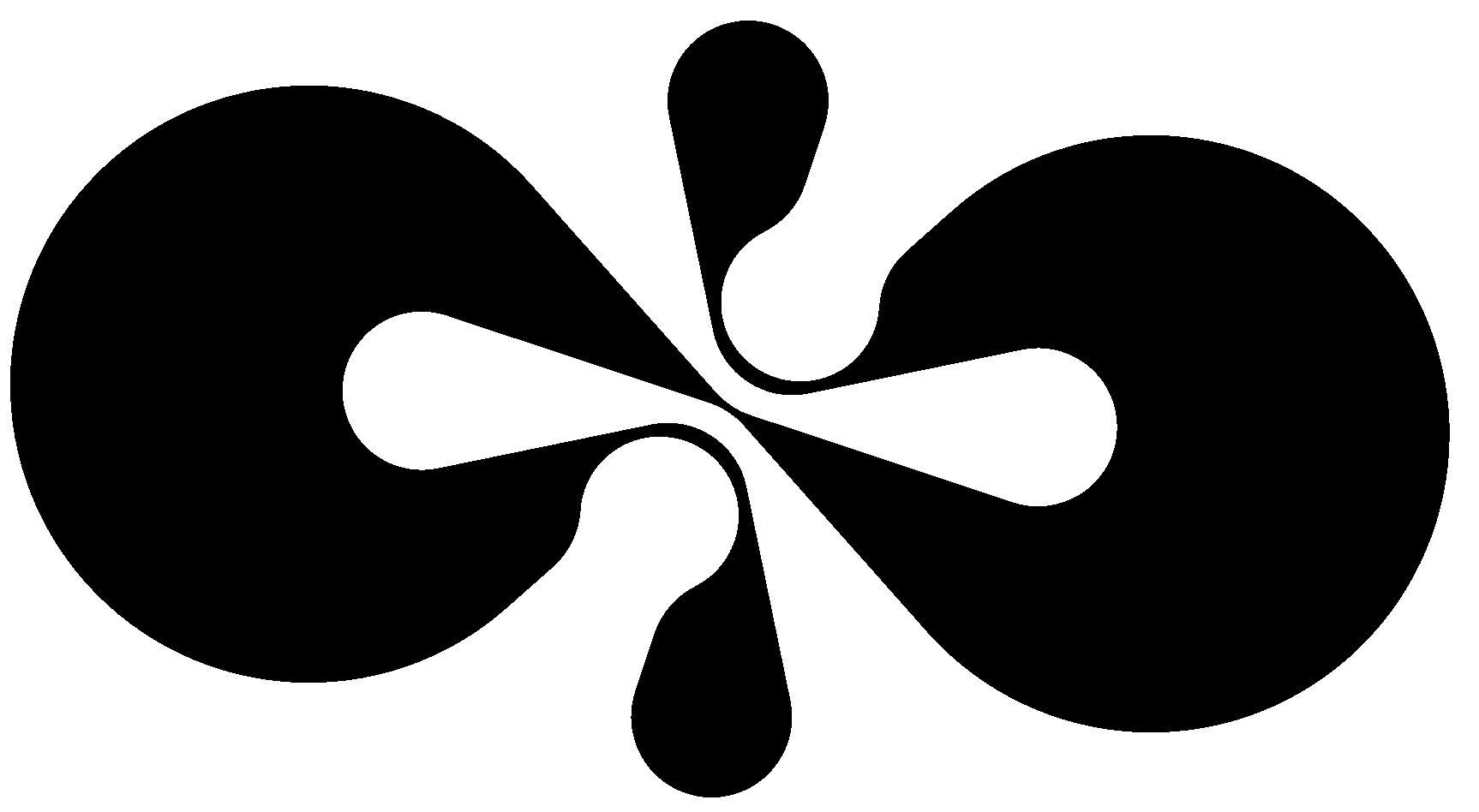  |
What can you draw? What can you draw? Your canvas is the plane − colored white to begin with − and you are given two tools to draw with: a pencil, which produces a black unit disk wherever it meets the canvas, and an eraser, which produces a white unit disk. There are no further restrictions on your artistic freedom: You may raise the tool off the canvas, that is, there is no continuity requirement for the centers of disks you draw, and you can switch tools as many times as desired. We show that drawability has global obstructions that is large portions of a set in the plane may be indistinguishable from a drawable set, yet globally the set cannot be drawn. |
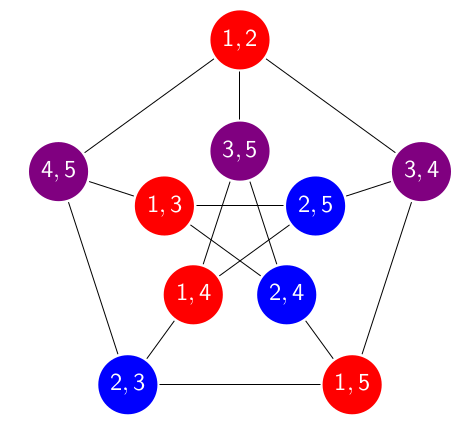 |
On the generalized Erdős−Kneser conjecture: Proofs and reductions How many colors are needed to color all k-element subsets of {1,2,...,n} such that disjoint sets receive distinct colors? This question was answered by Laszlo Lovasz. Erdos more generally raised the question how many colors are needed such that in any collection of r such sets, where any s have empty intersection, we see more than one color. In this paper we settle almost all remaining cases of this problem by reducing it to a multiple-coincidence problem for continuous maps and employing topological methods. |
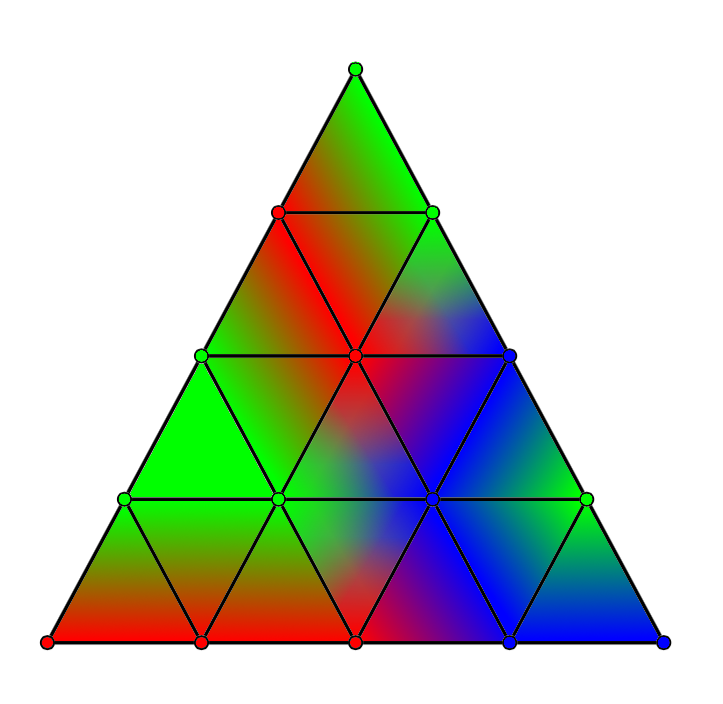 |
Fair division and generalizations of Sperner- and KKM-type results We address problems of fair division. For example, if n roommates with subjective preferences move into an n-bedroom apartment, can the rent be divided among the rooms such that roommates prefer pairwise distinct rooms. This results in an envy-free rent division. This is still possible if the preferences of one roommate are unknown at the point where the rent division is decided. We approach this problem by proving "colorful" generalizations of Brouwer's fixed point theorem. |
 |
On the number of edges in maximally linkless graphs A graph is linkless if it can be placed within 3-space such that no two cycles are linked with one another. A graph is maximally linkless if it is linkless and adding any edge necessarily creates a non-trivial link. In this project, Max constructs a sequence of maximally linkless graphs with fewer than 14n/5 edges. Surprisingly, these graphs are sparser than maximally planar graphs. |
... and several more
Topological methods in zero-sum Ramsey theory
by Florian Frick, Jacob Lehmann Duke, Meenakshi McNamara, Hannah Park-Kaufmann, Steven Raanes, Steven Simon, Darrion Thornburgh, and Zoe Wellner
16 pages, Preprint
Borsuk−Ulam theorems for products of spheres and Stiefel manifolds revisited
by Yu Hin Chan, Shujian Chen, Florian Frick, and J. Tristan Hull
Topol. Methods Nonlinear Anal. 55 (2), 553−564 (2020)
Transversal generalizations of hyperplane equipartitions
by Florian Frick, Samuel Murray, Steven Simon, and Laura Stemmler
Int. Math. Res. Not. IMRN (2023), to appear
Embedding dimensions of simplicial complexes on few vertices
by Florian Frick, Mirabel Hu, Verity Scheel, and Steven Simon
Ann. Comb. 27, 993−1003 (2023)
Fair splittings by independent sets in sparse graphs
by Alexander Black, Umur Cetin, Florian Frick, Alexander Pacun, and Linus Setiabrata
Israel J. Math. 236, 603−627 (2020)
arXiv version
On Reay's relaxed Tverberg conjecture and generalizations of Conway's thrackle conjecture
by Megumi Asada, Ryan Chen, Florian Frick, Frederick Huang, Maxwell Polevy, David Stoner, Ling Hei Tsang, and Zoe Wellner
Electronic J. Combin. 25 (3), P3.16, 14 pages (2018)
arXiv version
