One approach to achieve this is to change the basis representing the design space such that
one is using orthonormal decomposition. For the shape design
problem it means that
we use a basis of shape functions ![]() where the representation of the
shape is
where the representation of the
shape is
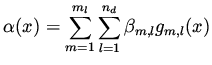 |
(46) |
The idea is that these new shape functions, ![]() are going to be of
increasing oscillations, due to their orthogonality. This implies that their effect on the solution will also be of increasing oscillations.
Thus, we achieve a decomposition of the design space into
subspaces of different smoothness as far as its effect on the solution.
The implication of this is that
a natural preconditioner of the
optimization process is done.
Since each level of those coarse grids on which optimization is to be done
works independently of the other,
at the relaxation step, we have removed the bad conditioning
from the problem using this decomposition.
The relaxation of the design variables is done now for the
are going to be of
increasing oscillations, due to their orthogonality. This implies that their effect on the solution will also be of increasing oscillations.
Thus, we achieve a decomposition of the design space into
subspaces of different smoothness as far as its effect on the solution.
The implication of this is that
a natural preconditioner of the
optimization process is done.
Since each level of those coarse grids on which optimization is to be done
works independently of the other,
at the relaxation step, we have removed the bad conditioning
from the problem using this decomposition.
The relaxation of the design variables is done now for the ![]() instead of the original
instead of the original ![]() . On level
. On level ![]() we update
we update ![]() of the
total design variables,
of the
total design variables,
![]() .
.
Relaxation: Level ![]()
![]() (1) Relax State Equation
(1) Relax State Equation
![]() (2) Relax Adjoint Equation
(2) Relax Adjoint Equation
![]() (3) Update design variables
(3) Update design variables
![]()