


Next: Condition Number of the
Up: Review of The Basics:
Previous: Unconstrained Optimization
Consider next the problem
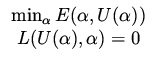 |
|
|
(5) |
where
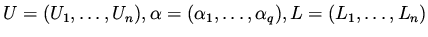 . We derive now the optimality conditions for this case.
Consider changes in
. We derive now the optimality conditions for this case.
Consider changes in 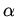 and correspondingly in
and correspondingly in 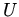 as
as
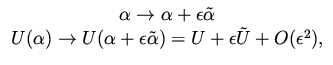 |
|
|
(6) |
where 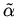 and
and 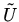 are related through the equation
are related through the equation
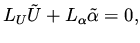 |
|
|
(7) |
which is a linearization of the constraint equation in (5).
The variation in the functional can be written as
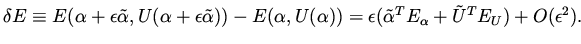 |
|
|
(8) |
For this formulation we see that a descent direction
for the functional depends on 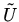 , which is not known before we have
decided about the direction of change (since
, which is not known before we have
decided about the direction of change (since 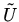 depends on
depends on 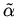 ).
Using
).
Using 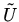 is not a viable approach and we are going to derive
a different one.
The idea is to eliminate the dependence of the variation
in the functional on
is not a viable approach and we are going to derive
a different one.
The idea is to eliminate the dependence of the variation
in the functional on 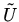 . We derive it in details since later on we need to do a similar
derivation for partial differential equations (PDE) and there things may look less
obvious.
. We derive it in details since later on we need to do a similar
derivation for partial differential equations (PDE) and there things may look less
obvious.
From equation (7) for 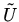 we have (by taking transpose),
we have (by taking transpose),
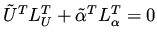 |
|
|
(9) |
and therefore also
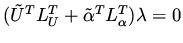 |
|
|
(10) |
for an arbitrary vector
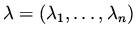 .
The plan is to add this term, which is zero, to our expression for the variation in
the cost functional and then by using a proper choice for
.
The plan is to add this term, which is zero, to our expression for the variation in
the cost functional and then by using a proper choice for 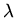 simplifying the variation of the cost functional such that it does not depend on
simplifying the variation of the cost functional such that it does not depend on 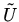 .
Clearly,
.
Clearly,
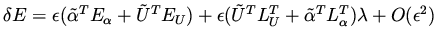 |
|
|
(11) |
and by recombination of terms
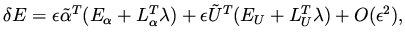 |
|
|
(12) |
and this is true for all 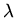 . Now a proper choice for
. Now a proper choice for 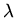 that simplifies (12) is given by
that simplifies (12) is given by
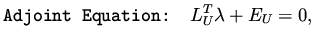 |
|
|
(13) |
which leads to
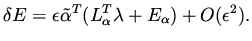 |
|
|
(14) |
Equation (13) for 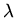 is called the adjoint (or costate) equation and
is called the adjoint (or costate) equation and
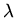 is called the adjoint (costate) variable, or the Lagrange multiplier.
Note the last expression for the variation of
is called the adjoint (costate) variable, or the Lagrange multiplier.
Note the last expression for the variation of 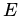 given by (14) does not depends on
given by (14) does not depends on
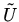 , but it does depends on
, but it does depends on 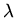 , which satisfies the adjoint
equation listed above.
It is clear that the choice
, which satisfies the adjoint
equation listed above.
It is clear that the choice
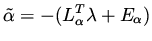 |
|
|
(15) |
is a direction of descent for the functional 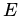 , since
, since
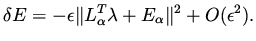 |
|
|
(16) |
This direction is called the steepest descent direction, and the method based
on it is called the steepest descent method.
At a minimum
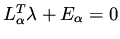 , giving us the optimality condition (necessary condition)
, giving us the optimality condition (necessary condition)
 |
|
|
(17) |
The left hand side of the last equation is the gradient of the functional subject to the constraints,
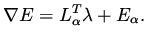 |
|
|
(18) |



Next: Condition Number of the
Up: Review of The Basics:
Previous: Unconstrained Optimization
Shlomo Ta'asan
2001-08-22
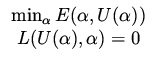
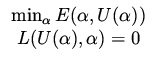
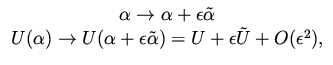
![]() , which is not known before we have
decided about the direction of change (since
, which is not known before we have
decided about the direction of change (since ![]() depends on
depends on ![]() ).
Using
).
Using ![]() is not a viable approach and we are going to derive
a different one.
The idea is to eliminate the dependence of the variation
in the functional on
is not a viable approach and we are going to derive
a different one.
The idea is to eliminate the dependence of the variation
in the functional on ![]() . We derive it in details since later on we need to do a similar
derivation for partial differential equations (PDE) and there things may look less
obvious.
. We derive it in details since later on we need to do a similar
derivation for partial differential equations (PDE) and there things may look less
obvious.
![]() we have (by taking transpose),
we have (by taking transpose),
![]() , giving us the optimality condition (necessary condition)
, giving us the optimality condition (necessary condition)
