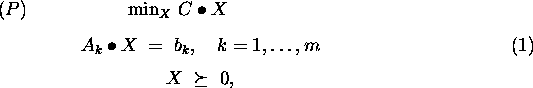
This is a software package for solving the standard SDP:
where 
, 
and
are given data,
and 
is the variable, possibly complex.
Here 
denotes the space of
hermitian matrices, 
denotes
the inner product 
, and 
means that X is positive semidefinite.
We assume that the set 
is linearly independent.
(If this set is nearly dependent, transformation to a better-conditioned
basis may be advisable for numerical stability.)
The software also solves the dual problem associated with (P):
where 
and 
are the variables.
This package is written in MATLAB version 5.0. It is available from the internet site:
http://www.math.nus.sg/~mattohkc/index.html
The purpose of this software package is to provide researchers in SDP with a collection of reasonably efficient algorithms that can solve general SDPs with matrices of dimensions of the order of a hundred. If your problem is large-scale, you should probably use an implementation that exploits problem structure. The only structure we exploit in this package is block-diagonal structure, where MATLAB cell arrays are used to handle dense and sparse blocks separately. For the purpose of evaluating the performance of algorithms proposed by other authors, we also include a few classes of SDP problems in this software package.
A special feature that distinguishes this SDP software from
others (e.g., [3],[4],[5],[10])
is that complex data are
allowed. But note that b and y must be real.
Another special feature, though also shared by the software of
[5], of our package is that the sparsity of matrices
is exploited in the computation of the Schur complement
matrix required at each iteration of our SDP algorithms.
Part of the codes for real symmetric matrices is originally based on those by Alizadeh, Haeberly, and Overton, whose help we gratefully acknowledge.
