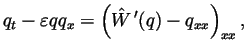Carnegie Mellon
Department of Mathematical Sciences

Stephen J. Watson, Engineering Sciences and Applied Math, McCormick School of Engineering and Applied Science, Northwestern University.

"Coarsening dynamics of the convective Cahn-Hilliard equation and faceted crytal growth"

Abstract

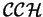The coarsening dynamics of a faceted vicinal crystalline surface growing into its melt by attachment kinetics is considered. The convective Cahn-Hilliard equation ( $ \mathcal{CCH}$) is derived as a small amplitude expansion of such surface evolutions restricted to 1-D morphologies. It takes the form

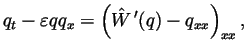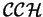$\displaystyle q_t - \varepsilon q q_x = \left( \hat{W}^{\,\prime} (q) - q_{xx} \right)_{xx},$ ( $ \mathcal{CCH}$)

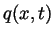
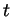
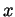
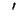
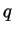
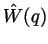
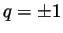
where the local surface slope $ q(x,t)$ serves as the order parameter, subscripts denote partial derivative with respect to time $ t$ and space $ x$ respectively, and $ \ ^{\,\prime}$ denotes the $ q$-derivative. The effective free energy $ \hat{W}(q) $ takes the form of a symmetric double well with minima at $ q= \pm 1 $, thereby capturing the anisotropy of the crystal surface energy. 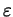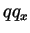Also, the dimensionless small parameter $ \varepsilon$ multiplying the convective term $ q q_x$ is a dimensionless measure of the growth strength.

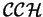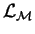A sharp interface theory for $ \mathcal{CCH}$ is derived through a matched asymptotic analysis. The theory predicts a nearest neighbor interaction between two non-symetrically related phase boundaries (kink and anti-kink), whose characteristic separation $ \mathcal{L}_{\mathcal{M}}$ grows as coalescing kink/anti-kinks annihilate one another. Theoretical predictions on the resulting (skew-symetric) coarsening dynamical system 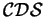$ \mathcal{CDS}$ include

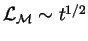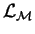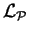  • The characteristic length $ \mathcal{L}_{\mathcal{M}} \sim t^{1/2}$, provided $ \mathcal{L}_{\mathcal{M}}$ is appropriately small with respect to the Peclet length scale $ \mathcal{L}_{\mathcal{P}}$.
  • Binary coalescence of phase boundaries is impossible
  • Ternary coalescence may only occur through the kink-ternary interaction; two kinks meet an anti-kink resulting in a kink.
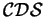
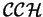
Direct numerical simulations performed on both $ \mathcal{CDS}$ and $ \mathcal{CCH}$ confirm each of these predictions.

Last, a linear stability analysis of 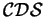$ \mathcal{CDS}$ identifies a pinching mechanism as the dominant instability, which in turn leads to kink-ternaries. We propose a self-similar period-doubling pinch ansatz as a model for the coarsening process, from which an analytical coarsening law for the characteristic length scale 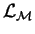$ \mathcal{L}_{\mathcal{M}}$ emerges. 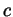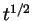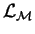It predicts both the scaling constant $ c$ of the $ t^{1/2}$ regime, i.e., 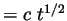$ \mathcal{L}_{\mathcal{M}}$ $ = c\ t^{1/2} $ , as well as the crossover to logarithmically slow coarsening as 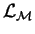$ \mathcal{L}_{\mathcal{M}}$ crosses 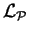$ \mathcal{L}_{\mathcal{P}}$. 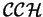Our analytical coarsening law stands in good qualitative agreement with large scale numerical simulations that have been performed on $ \mathcal{CCH}$.

In part, joint work with Felix Otto and Stephen H. Davis.

April 15, 2003
Time: 4:30 P.M.
Location: PPB 300

PLEASE NOTE TIME.

Mathematical Sciences Home      Mellon College of Science       Carnegie Mellon University