Abstract
To fix ideas, let
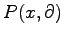 be a linear differential operator on
be a linear differential operator on
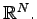 The lecture will center on the following question: Suppose that
a given right-hand side
The lecture will center on the following question: Suppose that
a given right-hand side 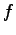 has ``some'' type of decay at infinity. How much
of that decay is inherited by the solutions
has ``some'' type of decay at infinity. How much
of that decay is inherited by the solutions 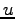 of
of
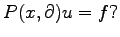
Among other things, the answer to this question will require the specification
of a functional setting and a suitable definition of what is meant by ``type
of decay''. A good functional setting is given by the Sobolev spaces
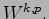 The suitable definition for the type of decay involves the choice
of a smooth positive function
The suitable definition for the type of decay involves the choice
of a smooth positive function 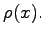 Then,
Then,
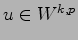 has decay of
type
has decay of
type 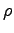 if
if
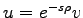 for some
for some 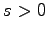 and some
and some
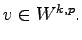 For
instance, if
For
instance, if
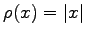 for
for 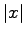 large enough, the corresponding type of
decay is exponential type. On the other hand,
large enough, the corresponding type of
decay is exponential type. On the other hand,
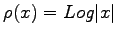 for
for 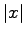 large enough corresponds to power-like decay. In all cases, while
large enough corresponds to power-like decay. In all cases, while 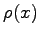 characterizes the type of decay of interest, the parameter
characterizes the type of decay of interest, the parameter 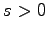 measures the
amount of such decay.
measures the
amount of such decay.
The above definition of decay, which is not the usual one, leads to a very
simple and general result: If the operator
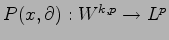 is Fredholm (of any index) and if, roughly speaking,
is Fredholm (of any index) and if, roughly speaking, 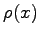 does
not grow faster than
does
not grow faster than 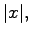 then every solution
then every solution
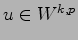 of
of
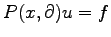 inherits at least part of the decay of
inherits at least part of the decay of 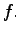 In
particular, this can be used with
In
particular, this can be used with 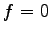 to establish the exponential decay
of eigenfunctions and generalized eigenfunctions (no selfadjointness is
required) corresponding to Fredholm eigenvalues. Furthermore, the principle
is easily extended to nonlinear operators and is not limited to the elliptic
case. Variants when
to establish the exponential decay
of eigenfunctions and generalized eigenfunctions (no selfadjointness is
required) corresponding to Fredholm eigenvalues. Furthermore, the principle
is easily extended to nonlinear operators and is not limited to the elliptic
case. Variants when
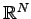 is replaced by another domain give
information about the boundary behavior of the solutions in terms of the
boundary behavior of the right-hand sides. In fact, everything follows from an
abstract result in reflexive Banach spaces, with no reference whatsoever to
partial differential equations. However, as well known examples show, the
Fredholm assumption is crucial.
is replaced by another domain give
information about the boundary behavior of the solutions in terms of the
boundary behavior of the right-hand sides. In fact, everything follows from an
abstract result in reflexive Banach spaces, with no reference whatsoever to
partial differential equations. However, as well known examples show, the
Fredholm assumption is crucial.
TUESDAY, January 16, 2007
Time: 1:30 P.M.
Location: PPB 300