Abstract

The Skyrme model (1961) was one of the first attempts to describe elementary particles as localized in space solutions of nonlinear PDEs. The fields take their values in 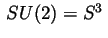and stabilize at spatial infinity. Thus, the configuration space splits into different sectors (homotopy classes) with a constant topological charge (the degree) in each sector.

In this talk I will discuss the existence of minimizers for the Skyrme energy functional. Also, I will consider two generalizations of the Skyrme model: one is a variational problem for maps from a compact 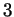-manifold to a compact Lie group; the other is a variational problem for flat connections. I will describe the path components of the configuration spaces of smooth fields for each of the variational problems. The invariants separating the path components are the Chern-Simons invariant and a holonomy representation. It turns out that the Chern-Simons invariant is well defined for connections with finite Skyrme energy. 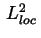As for holonomy, we have to define it in such a way that the definition is valid for distributionally flat connections. In particular, our definition is valid for flat connections with bounded Skyrme energy. The key analytical result here is a nonlinear Poincaré lemma.

TUESDAY, November 18, 2003
Time: 1:30 P.M.
Location: PPB 300