Stuart Hasting, Dept. of Mathematics, University of Pittsburgh

" Layers, chaos, and global attractors for some one-dimensional reaction diffusion problems"

Abstract

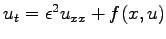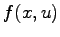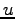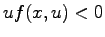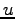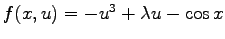We consider equations of the form $u_t=\epsilon^2 u_{xx}+f(x,u)$ with Neumann boundary conditions. The key early reference is by Angenent, Mallet-Paret and Peletier (1987), who found all stable equilibrium solutions for a class of function which are cubic in , with for large . In joint work with S.B. Ai we study the ``Duffing'' case $f(x,u)=-u^3+\lambda u-\cos x$ , and find a large class of unstable equilibria, including solutions with multiple internal layers. 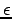We also study the ode satisfied by the steady states as a nonlinear oscillator, and obtain some chaos results which do not treat $\epsilon$ as a small parameter.

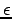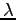In the case of the Neumann problem for small $\epsilon$ we are able to obtain the Morse index of the new solutions. Further, we consider the bifurcation of solutions as a function of $\lambda$ , and we anticipate that near the initial bifurcation point it will be possible to apply techniques of Fiedler and Rochas to determine the global attractor.

TUESDAY, October 31, 2000
Time: 1:30 P.M.
Location: PPB 300

Mathematical Sciences Home Mellon College of Science Carnegie Mellon University