Irene Fonseca, Department of Mathematical Sciences, Carnegie Mellon University

"Micromagnetics : Equilibria and Relaxation"

Abstract

Minima of the energy for large magnetic bodies with vanishing induced magnetic fields

$\displaystyle E(m):=\int_{\Omega }[\varphi (m)-\langle h_{e};m\rangle ]\,dx+\frac{1}{2} \int_{\mathbb{R}^3}\vert h_{m}\vert^{2}\,dx$

(1)

are completely characterized in terms of the anisotropic energy density 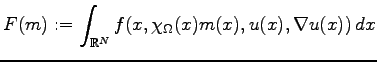$\varphi$ and the applied external magnetic field $h_{e}\in \mathbb{R}^3$ . More generally, one considers an energy functional for a large ferromagnetic body of the form

$\displaystyle F(m) :=\int_{\mathbb{R}^N} f(x, \chi_{\Omega}(x) m(x), u(x), \nabla u(x))\, dx$

where $(\chi_{\Omega} m, \nabla u)$ satisfies Maxwell's equations, i.e. $u \in H^1(\mathbb{R}^N)$ is the unique solution of $\Delta u + {\rm div}\, (\chi_{\Omega} m) = 0$ in $\mathbb{R}^N$ . It is shown that if

is a Carathéodory function satisfying very mild growth conditions then the relaxation of

with respect to $L^{\infty}-w*$ convergence in $L^{\infty}(\Omega;\overline{B(0,1)})$ is given by

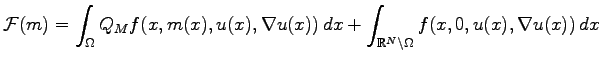
$\displaystyle {\cal F}(m) = \int_{\Omega} Q_M f(x,m(x),u(x),\nabla u(x))\, dx + \int_{\mathbb{R}^N \setminus \Omega} f(x,0,u(x),\nabla u(x))\, dx$

where

is the quasiconvex envelope of

relative to the underlying partial differential equations. This class of integrands includes those of the type

$\displaystyle f(x,m,u,h) = \varphi(x,m,u) + \psi(x,u,h)$

with $\psi(x,u,\cdot)$ non convex.

The first part of this work was undertaken in collaboration with Bernard Dacorogna and the relaxation results were obtained jointly with Giovanni Leoni.

TUESDAY, January 30, 2001
Time: 1:30 P.M.
Location: PPB 300

Mathematical Sciences Home Mellon College of Science Carnegie Mellon University