Eitan Tadmor, Center for Scientific Computation and mathematical Modeling (CSCAMM), Department of Mathematics and Institute for Physical Science & Technology, University of Maryland.

"Critical Thresholds in Eulerian Dynamics "

Abstract

We study the questions of global regularity vs. finite time breakdown in Eulerian dynamics, 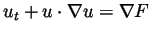$u_t + u \cdot \nabla u = \nabla F$ , which shows up in different contexts dictated by modeling of 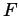's. To address these questions, we propose the notion Critical Threshold (CT), where a conditional finite time breakdown depends on whether the initial configuration crosses an intrinsic, 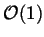${\cal O}(1)$ critical threshold. Our approach is based on a main new tool of spectral dynamics, where the eigenvalues, 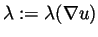$\lambda := \lambda (\nabla u)$ , and eigenpairs 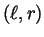$(\ell,r)$ , are traced b y the forced Raccati equation 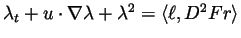$\lambda_t + u \cdot \nabla \lambda + \lambda^2 =\left<\ell,D^2Fr\right>$ . We shall outline three prototype cases.

We begin with the 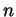-dimensional Restricted Euler equations, obtaining global invariants which precisely characterize the local topology at breakdown time. Next we introduce the corresponding -dimensional Restricted Euler-Poisson (REP) system, identifying a set of global invariants, which yield (i) sufficient conditions for finite time breakdown, and (ii) a remarkable characterization of two-dimensional initial REP configurations with global smooth solutions. And finally, we show that a CT phenomenon associated with rotation prevents finite-time breakdown. 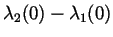Our study reveals the dependence of the CT phenomenon on the initial spectral gap, $\lambda_2(0)-\lambda_1(0)$ .

THURSDAY, April 1, 2004
Time: 1:30 P.M.
Location: PPB 300

Mathematical Sciences Home Mellon College of Science Carnegie Mellon University