Abstract
It is well-known that Morrey's quasiconvexity is closely related to gradient Young measures,
i.e., Young measures generated by sequences of gradients in
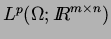
. Concentration effects,
however, cannot be treated by Young measures. One way how to describe both oscillation and
concentration effects in a fair generality are the so-called DiPerna-Majda measures.
DiPerna and Majda showed that having a sequence 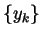 bounded in
bounded in
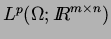 ,
,
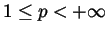 , and a complete separable subring
, and a complete separable subring 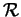 of continuous bounded functions on
of continuous bounded functions on
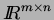 then there exists a subsequence of
then there exists a subsequence of 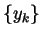 (not relabeled),
a positive Radon measure
(not relabeled),
a positive Radon measure 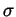 on
on 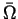 , and a family of probability
measures on
, and a family of probability
measures on
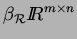 (the metrizable compactification of
(the metrizable compactification of
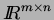 corresponding to
corresponding to 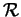 ),
),
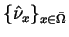 , such that
for all
, such that
for all
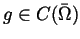 and all
and all
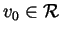
where
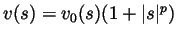
.
Our talk will address the question:
What conditions must
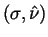 satisfy,
so that
satisfy,
so that
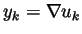 for
for
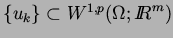 with
with 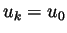 on
on
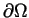 ?
? We are going to state necessary and sufficient conditions.
We will mainly work with
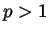
, however, special cases for
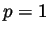
will be
discussed, as well.
TUESDAY, April 25, 2006
Time: 1:30 P.M.
Location: PPB 300