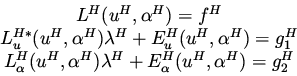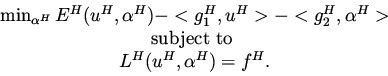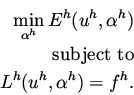
Consider the minimization problem
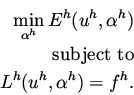
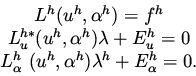
Next consider an attempt to define a coarse grid minimization problem that will accelerate the convergence of the fine grid above. We will show that without the use of Lagrange multipliers this is in general impossible. An argument for a quadratic functional and linear constraint is given in Ta'asan [7]. Consider the coarse grid minimization problem
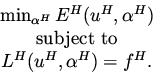
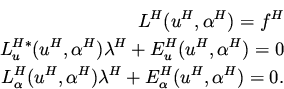
In order for this coarse grid equation to accelerate the fine grid solution
process
we must have the property that if the fine grid equations are solved, the coarse
grid will not introduce any change to the fine grid solution.
This means that the coarse grid function
![]() must satisfy the
coarse grid equation (Recall that the interpolation step is using the
correction
must satisfy the
coarse grid equation (Recall that the interpolation step is using the
correction
![]() ).
From the first equation we see that we must have
).
From the first equation we see that we must have
![]() , and
from the second and third coarse grid necessary condition we see that there
must exists a function
, and
from the second and third coarse grid necessary condition we see that there
must exists a function ![]() that satisfies simultaneously the two equation
that satisfies simultaneously the two equation
![]() and
and
![]() .
But since the the two right hand sides are independent, in general, we have twice
the number of equations than the number of unknowns in
.
But since the the two right hand sides are independent, in general, we have twice
the number of equations than the number of unknowns in ![]() .
Thus, in general
.
Thus, in general
![]() will not be the solution of the coarse grid minimization problem.
will not be the solution of the coarse grid minimization problem.
The correct way to define the coarse grid minimization problem is to start with the FAS equations for the necessary conditions. Thus, we get