Authors: Gautam Iyer, Alexander Kiselev and Xiaoqian Xu.

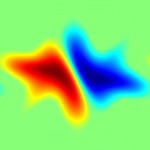
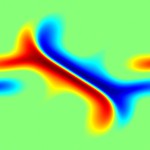
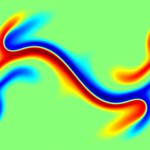
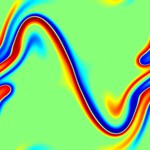
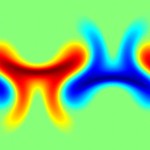
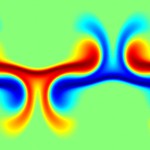
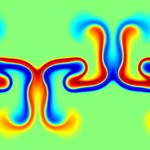
This page contains code, simulations and a brief summary of our results in (1). Our aim is to study how well temperature in a fluid can be mixed by an incompressible, enstrophy constrained flow. Here are some figures showing particular initial distributions getting optimally mixed.

Note the difference between the initial data in the first and second set of figures above is very slight. In the first one, the red blob is slightly closer to the blue blob than it is to the (periodic) boundary. In the second one the red blob is exactly as far away from the blue blob as it is from the (periodic) boundary. In the second case the optimal mixing strategy moves divides the red blob symmetrically, and in the first case it does not.

Brief Mathematical Description

Mathematically the above problem of mixing reduces to studying the equation $$ \delt \theta + u \cdot \grad \theta = 0, $$ and choosing $u$ to be an incompressible vector field that minimizes $\norm{\theta}_ {H^{-1}}$. Our main result shows that if $u$ is enstrophy constrained (e.g. $\norm{u}_ {H^{-1}}=F$), then $\norm{\theta}_ {H^{-1}}$ decays at most exponentially with time. Precisely if $\theta_0$ is mean zero and only takes on the values ${0, \pm 1}$, then we show \begin{equation}\label{eqnTheta} \norm{\theta(t)}_ {H^{-1}} \geq \eps_0 r_0^{2} \exp \paren[\Big]{ \frac{-c}{m \paren{ \supp(\theta_0) }^{1/2} } \int_0^t \norm{\grad u(s)}_ {L^2} \, ds }. \end{equation} for some constants $\eps_0$ and $c$. Here $r_0$ is a length scale associated to the initial data. (More details and our main result (which is more general) can be found in (1).)

Numerical simulations

Previous work of (2) shows that the incompressible velocity field $u$ with $\norm{\grad u}_ {L^2} = 1$ that maximises $-\delt \norm{\theta}_ {H^{-1}}$ is explicitly given by \begin{equation}\label{eqnU} u=\frac{-\lap^{-1}P(\theta\nabla^{-1}\theta)}{\norm{\nabla^{-1}P(\theta\nabla^{-1}\theta)}_ {L^2}}, \end{equation}

Our numerics solve equation \eqref{eqnTheta} where $u$ is computed using equation \eqref{eqnU} using a pseudo-spectral method. The code used to generate these figures can be downloaded here. Instructions for running the code can be found in the Readme.md file.