When calculating the derivative of y=f(x) one needs to carry out 4 steps:

1) Write down the difference quotient

2) Use the definition of f to evaluate the difference quotient at f

3) Simplify the difference quotient

4) Take the limit of the difference quotient as h goes to 0

To do this, we enter the difference quotient into Maple once and for all in this lab:

> A:=(f(x+h)-f(x))/h;

Next we load a student package that allows us to evaluate the difference quotient at any function f:

> dq:=student[makeproc](A,f);

For example, let's take a simple function and carry out the 4 steps:

> f:=x->x^4;

> dq(f);

> simplify(dq(f));

MAPLE expanded the binomial, canceled terms and divided the h off. Let's see that this is what happened.

> expand((x+h)^4);

> (%-x^4)/h;

> simplify(%);

as before.

> Limit(%,h=0);value(%);

We can check our answer using the built-in function that calculates the derivative of f:

> D(f);

Let's go through a variety of examples that you should be able to do by hand:

> f:=x->2*x^2-5*x+11;

> dq(f);

> simplify(dq(f));

> Limit(%,h=0);

> value(%);

Note that with the square root function MAPLE does not display the independent variable x. This is always

the case for built-in function:

> f:=x->sqrt(x);

> dq(f);

> simplify(%);

Notice that simplify does nothing in this case. In order to simplify to be able to do calculate

limit as h goes to zero, you need to conjugate. We can force MAPLE to do this manually. You need lots

of brackets and make sure that MAPLE expands the numerator as a difference of squares:

> expand((sqrt(x+h)-sqrt(x))*(sqrt(x+h)+sqrt(x)))/((sqrt(x+h)+sqrt(x))*h);

> Limit(%,h=0);value(%);

Here is a popular example which manually involves getting a common denominator:

> f:=x->1/x;

> dq(f);

> simplify(dq(f));

> Limit(%,h=0);value(%);

Recall that when you calculate the derivative of the exponential function, you end up with a limit that

difficult to establish analytically:

> dq(exp);

> expand((exp(x+h)-exp(x))/h);

> factor(%);

Now when we take the limit as h goes to zero, we can take the term e^x out of the limit since

it is independent of h. This leads to the limit:

> Limit((exp(h)-1)/h,h=0);

Let's investigate this limit by looking at a graph:

> plot((exp(x)-1)/x,x=-10..10,y=0..2);

Let's ask MAPLE to find the limit:

> Limit((exp(x)-1)/x,x=0);value(%);

> Limit(dq(exp),h=0);value(%);

Finally we turn to the trigonometric function y=sin x.

> f:=sin;

> expand(dq(f));

> factor(sin(x)*cos(h)/h-sin(x)/h)+cos(x)*sin(h)/h;

Now when we take the limit of this as h goes to zero we use the fact that the limit of a sum is

the sum of limits and then pull out the terms independent of h. This leads to the two famous

trigonometric limits:

> Limit(sin(x)/x,x=0);Limit((cos(x)-1)/x,x=0);

In class we went through the detailed proof that the value of the first limit is 1 and the

value of the second limit is 0. The second follows from the first by multiplying top and

bottom by (cos(x)+1). Let's look at the graph of each of these to see if these limits look right.

> plot(sin(x)/x,x=-.1..0.1);

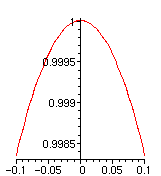
> Limit(sin (x)/x,x=0);value(%);

> plot((1-cos(x))/x,x=-10..10);

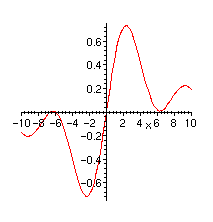
> plot((1-cos(x))/x,x=-0.1..0.1);

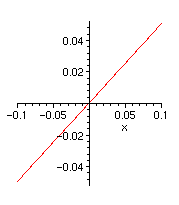
> Limit((1-cos(x))/x,x=0);value(%);