Symmetry is a very important concept in mathematics. A large part of mathematics is the identification and exploration of patterns, and symmetry is a pattern that appears over and over again in many places.
Here we will primarily examine geometric symmetry, but the concept of “symmetry” also appears in other forms. For example, in the game Tic-Tac-Toe, there are several kinds of symmetry. The geometric symmetries of the game board can be used to simplify the analysis of the game by allowing us to say, for instance, that there are essentially only three possible first moves: playing in the center square, playing in a corner square, or playing in a side square. (In reality, of course, there are nine possible first moves, but some of these moves are so similar to others, due to symmetry, that the same analysis applies to them all.) There is also symmetry between the two players—each player is playing under the same rules, has the same set of legal moves, and has the same information as the other player. This is not the case in all games. For example, in many fox games one player controls a single piece (usually called the “fox”) while the other player controls many pieces (often called “geese” or “sheep”).
We also used a broader concept of “symmetry” when we looked at the following question: Can an 8 × 8 checkerboard with opposite corner squares removed be tiled with dominoes? We saw that it cannot, because the two removed squares will be of the same color (if the checkerboard is colored in the usual way), so there will be more squares remaining of one color than of the other; but each domino must cover one square of each color. This answer to the question contrasts the asymmetry between the two colors on the checkerboard with the necessary symmetry of each domino.
For two-dimensional geometric shapes, there are four fundamental types of symmetry: reflection symmetry, rotation symmetry, translation symmetry, and glide symmetry.
A shape has reflection symmetry when it can be mirrored about a line and look the same as it did before.
A shape has rotation symmetry if it can be rotated about a point (by some angle less than 360°) and look the same as it did before. Of course every shape can be rotated by 360° and look the same; we don‘t usually consider this uninteresting case to be an example of rotation symmetry.
A shape has translation symmetry if it can be shifted some distance in some direction and match up with its previous image.
A fourth type of two-dimensional symmetry exists, though it is more subtle than the other three. It is called glide symmetry. A shape has glide symmetry if it can be shifted some distance in some direction (as for translation symmetry) and then mirrored about a line (as for reflection symmetry), and match up with its previous image.
Note that reflection symmetry implies one or more lines of symmetry, while rotation symmetry implies a point of symmetry and a (smallest) angle of rotation. Note also that translation symmetry and glide symmetry both require infinite shapes, such as an infinitely long strip or an infinite plane. Finite shapes cannot have these types of symmetry.
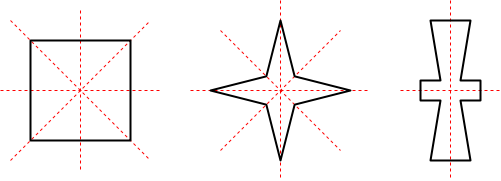
Shapes can be classified according to their symmetry. To do so (for finite shapes, like polygons), count the number of lines of (reflection) symmetry, if any, and determine the (smallest) angle of rotation symmetry, if any. For example, the first two of the following shapes each have exactly four lines of reflection symmetry, and their smallest angle of rotation symmetry is 90°; therefore they have the same kind of symmetry, and are classified together. On the other hand, the third shape does not have the same kind of symmetry, because it has only two lines of reflection symmetry, and its smallest angle of rotation symmetry is 180°.

A tiling, also called a tessellation, is a covering of a flat surface by nonoverlapping shapes with no gaps between them. Often, unless otherwise specified, the flat surface to be tiled is taken to be an infinite plane.
A polygon is a plane figure (that is, a shape drawn in a flat plane) whose boundary consists of three or more straight line segments. In particular, shapes with curved sides are not polygons. These line segments are called the edges of the polygon, and the points where two edges meet are called the vertices of the polygon. (The singular form of the word vertices is vertex.)
A polygon with three sides is called a triangle. A triangle may be equilateral, meaning that all its sides are the same length (in the case of a triangle, this also means that all its angles are equal). A triangle is isosceles if it has two sides of the same length (and hence two equal angles). Note that it is a matter of opinion whether equilateral triangles should be considered isosceles triangles or not; some definitions require an isosceles triangle to have exactly two equal sides, while others require at least two sides. This distinction is not very important to us at the moment, so we will ignore it. (If it becomes important to you, perhaps when you are writing a solution to a homework problem, simply decide which definition you want to use and state your choice.) A triangle is called scalene if all three of its sides (and hence all three of its angles) are different from each other.
A polygon with four sides is called a quadrilateral. A quadrilateral having opposite sides parallel is called a parallelogram. In a parallelogram, opposite sides have the same length and opposite angles are equal. A quadrilateral having all four sides the same length is called a rhombus. Every rhombus is a parallelogram, but not every parallelogram is a rhombus. A quadrilateral having all four angles equal (that is, having four right angles) is called a rectangle. Again, every rectangle is a parallelogram, but not every parallelogram is a rectangle. A quadrilateral that is both a rhombus and a rectangle is a square.
The names for polygons having more than four sides come from the Greek prefixes for five, six, seven, and so on, attached to the root -gon, which means “angle.” So a polygon with five sides is called a pentagon, one with six sides is a hexagon, one with seven sides is a heptagon, one with eight sides is an octagon, and so on. If we need to be abstract, we can refer to a polygon having n sides as an n-gon.
A polygon is called a regular polygon if all of its sides have the same length and all of its angles are equal. Thus, a regular triangle is the same as an equilateral triangle, and a regular quadrilateral is the same as a square.
There are several useful ways to measure the angles at the vertices of a polygon. Perhaps the most natural measurement is the interior angle (or the internal angle), which is the angle formed on the inside of the polygon at a vertex by the two edges meeting there. Another useful angle measurement is the angle formed outside the polygon by extending one of the edges; this is called the exterior angle (or the external angle).
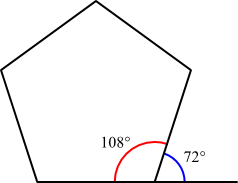
For example, consider the regular pentagon shown below. The interior angle at the lower right vertex is the larger of the two marked angles, which measures 108°. One of the exterior angles at the same vertex is the smaller marked angle, which measures 72°. (The other exterior angle at this vertex would be formed by extending the other edge of the pentagon instead; it would also measure 72°.) Note that together the interior angle and the exterior angle form a straight line, so their angle measures add up to 180°.
A polygon is said to be convex if, given any two points in the interior of the polygon, the straight line segment joining the two points does not leave the interior of the polygon. A polygon is nonconvex if it is not convex; that is, if there are two points in its interior such that the straight line segment joining them goes outside the polygon. An equivalent definition of convexity is the following: A polygon is convex if all its interior angles measure less than 180°.
It is useful to have formulas for the angle measures of regular polygons. To derive these formulas we begin by considering the exterior angles.
Imagine driving around the perimeter of a regular n-gon in a car. Whenever you reach a vertex, you must turn through some angle to continue along the next edge—this angle is exactly the exterior angle at that vertex. When you come back to your starting point, you will have turned your car through 360° in all. Since all of the n exterior angles are equal, because the n-gon is regular, each one must be 1/n of 360°. Therefore, we have the following formula:
(exterior angle of a regular
n-gon) =
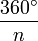 .
.
Now, since an interior angle and an exterior angle add up to 180°, we have
(interior angle of a regular
n-gon) =
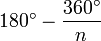 .
.
For our purposes, the formula above is the most important, because we will often be interested in the angle measure of interior angles of regular n-gons. While we’re at it, though, let’s find the total of all the interior angles of a regular n-gon. This is easy; since all of the n interior angles are equal, we can find the total by simply multiplying the measure of one interior angle by n. So we see that
(total of all interior angles of a regular
n-gon) =
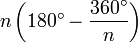 .
.
This formula is often presented in a slightly different form. By distributing the n and then factoring out 180°, we can write the formula above as
(total of all interior angles of a regular
n-gon) =
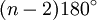 .
.
Using the formula for the measure of an interior angle of a regular n-gon, we can quickly compile the following table.
| n | Interior angle of regular n-gon |
|---|---|
| 3 | 60° |
| 4 | 90° |
| 5 | 108° |
| 6 | 120° |
| 7 | ≈ 128.57° |
| 8 | 135° |
| 9 | 140° |
| 10 | 144° |
| 11 | ≈ 147.27° |
| 12 | 150° |
Notice that as n gets larger, so does the measure of an interior angle. Since regular polygons are always convex, however, the measure of an interior angle of a regular n-gon must always be less than 180°.
Any parallelogram can tile the plane. Parallelogram tiles can easily be fit together to form a “slanted checkerboard” pattern, as shown below.

Any triangle can tile the plane. Take two copies of the triangle. Mark the same edge on each. Then fit them together by rotating one of them 180° and putting the marked edges together. This forms a parallelogram, which can then be repeated to tile the plane in a “slanted checkerboard” pattern as seen above.
Any hexagon in which each pair of opposite sides is parallel can tile the plane. Such hexagons can be fit together to form a “slanted honeycomb” pattern. It would be nice if there were a standard name for this kind of hexagon, but I don’t know of one. Perhaps they could be called “parallelohexagons” or “hexallelograms”?
A quadrilateral does not have to be a parallelogram to tile the plane. In fact, any quadrilateral can tile the plane. To do so, take two copies of the quadrilateral and mark the same edge on each. Then fit them together by rotating one of them 180° and putting the marked edges together, as we did for triangles. This forms a “parallelohexagon” which can tile the plane as described above.
We say that a tiling of the plane is an edge-to-edge tiling if it uses only polygons and adjacent tiles share full edges. For example, the pattern formed by the squares of a checkerboard is an edge-to-edge tiling, but the typical pattern formed by bricks in a wall is not.
We say that a tiling of the plane is vertex-transitive if it uses only polygons and every vertex (where three or more tiles come together) “looks like” every other vertex, in terms of the number, kind, and sequence of the shapes that surround it. For example, the tiling on the left below is vertex-transitive, because every vertex is surrounded by a triangle, a hexagon, a triangle, and a hexagon, in that order; but the tiling on the right is not vertex-transitive, because some vertices are surrounded by a triangle, a triangle, a hexagon, and a hexagon, in that order (the triangles are adjacent, and so are the hexagons), while others are surrounded by a triangle, a hexagon, a triangle, and a hexagon (the triangles are opposite each other, as are the hexagons).


A vertex of a tiling that uses regular polygons as tiles is sometimes described by a list of numbers, separated by periods, listing the numbers of sides in the tiles surrounding the vertex (in sequence). For example, if a vertex is surrounded by a triangle, a hexagon, a triangle, and a hexagon, in that order, it could be described as 3.6.3.6. Note that this is the same as 6.3.6.3, but it is different from 3.3.6.6, which would describe a vertex surrounded by a triangle, a triangle, a hexagon, and a hexagon, in that order. In the latter case the two triangular tiles would be adjacent, as would the two hexagonal tiles, whereas at a 3.6.3.6 vertex the two triangular tiles are opposite each other, and so are the two hexagonal tiles. If a tiling is vertex-transitive, then every vertex will be described by the same sequence of numbers. For brevity, consecutive identical numbers in such a sequence are sometimes written with exponent notation (so 3.3.6.6 might be written as 32.62).
A tiling of the plane is called a uniform tiling if it is an edge-to-edge tiling, it is vertex-transitive, and all the tiles are regular polygons.
A uniform tiling of the plane that uses only a single kind of regular polygon is called a regular tiling. In particular, a regular tiling is an edge-to-edge tiling, so the edges of the tiles must all be the same length and thus the regular polygons must all be the same size throughout the tiling.
If a uniform tiling is not a regular tiling, it is called a semiregular tiling. A semiregular tiling uses two or more kinds of regular polygons, for example, equilateral triangles and regular hexagons.
There are only three regular tilings of the plane. We can see this by examining the interior angles of the tiles surrounding any vertex. In any tiling, the total of these angles must be 360° (one full circle). So the tiles must have interior angles that can be added together to make 360°. Furthermore, at least three tiles must meet at each vertex (otherwise it wouldn’t be a vertex).
In a regular tiling, all of the tiles must be identical regular polygons. We have already figured out the measures of the interior angles of regular polygons. If three identical regular polygons meet at a vertex, the interior angle of each must be 360°/3 = 120°, which means that the polygons must be regular hexagons. If four identical regular polygons meet, their interior angles must be 360°/4 = 90°, which means that they must be squares (regular quadrilaterals). If five identical regular polygons were to meet at a vertex, their interior angles would have to be 360°/5 = 72°. But there is no regular polygon with interior angles of 72° (see the table above), so this is not possible. If six identical regular polygons meet at a vertex, their interior angles must be 360°/6 = 60°, so the polygons must be equilateral triangles. If seven or more identical regular polygons were to meet at a vertex, then their interior angles would need to be less than 60° (because we would be dividing 360° into more than six equal parts); but no regular polygon has interior angles less than 60°, so we conclude that this case is also impossible.
Therefore we see that the only possible regular tilings are ones in which three regular hexagons meet at each vertex, or four squares meet at each vertex, or six equilateral triangles meet at each vertex. These three regular tilings are shown below.



Similarly there are only eight semiregular tilings (though one of them, the 3.3.3.3.6 tiling shown first below, is not the same as its mirror image, so sometimes there are considered to be nine semiregular tilings). This can be established by considering the possible ways in which 360° can be written as a sum of interior angles of regular polygons. For example, one possibility is 360° = 60° + 90° + 120° + 90°, which gives the 3.4.6.4 semiregular tiling. The semiregular tilings are shown below.








A basic tiling, such as a regular or semiregular tiling or a tiling with “parallelohexagons,” can be modified to make a tiling that uses more complex shapes. To do so, we carefully modify the edges of the tiles by cutting pieces from one side and pasting them on somewhere else.
For example, suppose we begin with the “slanted checkerboard” tiling of parallelograms shown below.

We can modify these basic tiles by, say, adding a triangular point to the right-hand side, so long as we also cut a notch at the appropriate place in the left-hand side so that the tiles will still fit together:

Note the modification we have made to the fundamental tile: we have cut a triangular notch out of the left side and pasted it on the right side. We can continue this process, changing the shape of the tile bit by bit. With enough creativity and cleverness, the tile can be made to look like a person, an animal, a letter of the alphabet, or just about anything. Experiment! The tiling below, formed from an additional modification from the previous tiling, looks a little bit like a robot, perhaps. Of course it could use a few adjustments to look better.

This technique of modifying basic tilings was used by the Dutch graphic artist M. C. Escher to create some of his works of art. One example, called Horsemen (see http://www.tessellations.org/eschergallery18.htm), shows interlocking light and dark tiles shaped like horsemen. It would take a great deal of artistic vision, and quite a bit of trial and error, to create such a tiling, but the basic principle is the same as that used in the simple example above.
Wikipedia has several well-written articles about these topics, in particular:
David Patterson at the University of Montana has some notes (in PDF format) about symmetry and tilings available from his Math 105 page (see http://www.math.umt.edu/patterson/105/). These notes include many illustrations and examples of these concepts in nature and art.