Below are figures from several of my papers along with short annotations. I create figures in grayscale so that they are easily readable for colorblind readers, or readers who print in black and white. Additionally, it is an interesting challenge to clearly illustrate complicated objects without relying on color. The figures are shown in PNG format for web display, but vector art versions can be found in the corresponding papers.
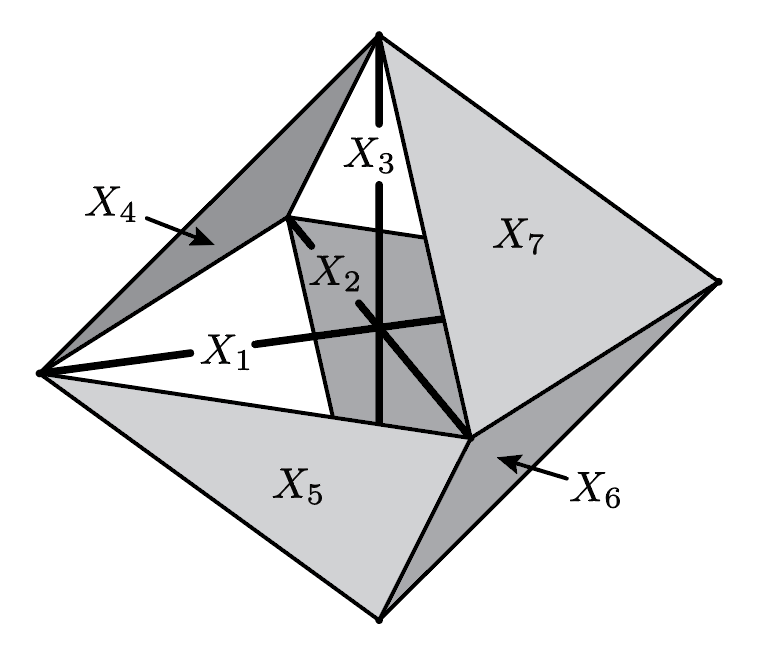Seven closed convex sets in 3-dimensional space, whose intersection pattern (i.e. code) records the incidences of points and lines the Fano plane. This code cannot be realized by closed convex sets in the plane, nor by open convex sets in 3-dimensional space. This appears as Figure 3 in "Embedding dimension gaps in sparse codes" which is joint work with Henry Siegel, David Staudinger, and Yiqing Wang.(click here to return to top)
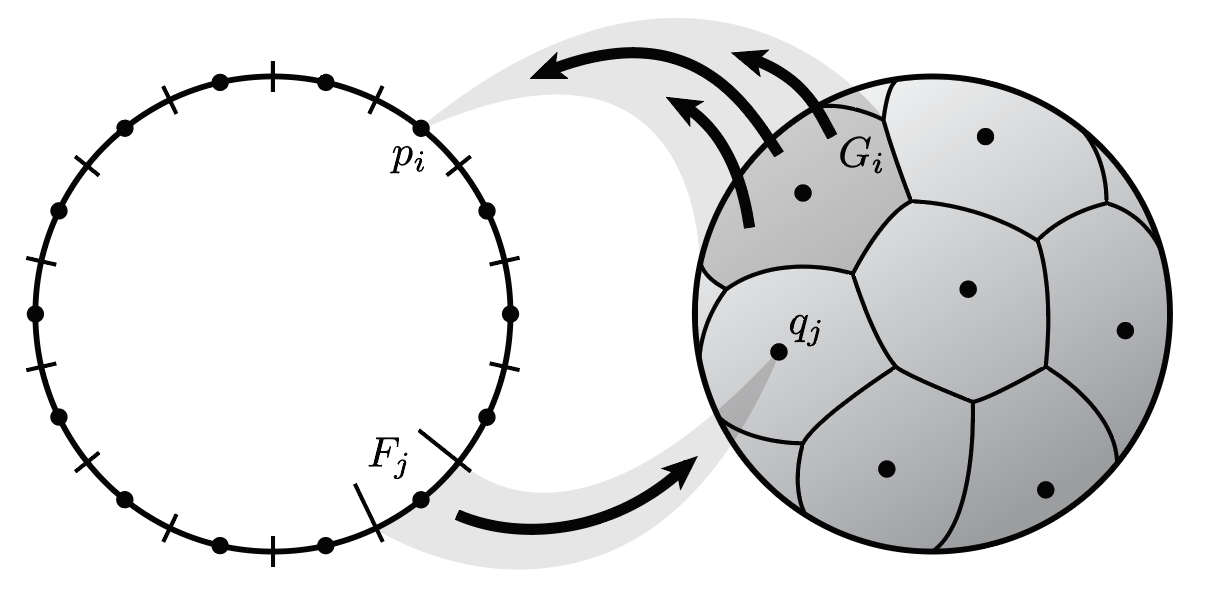An informal illustration of a correspondence between the n-sphere and the k-sphere, which provides quantitative upper bounds on the Gromov-Hausdorff distance between these spheres. This appears as Figure 1 in "Quantitative upper bounds on the Gromov-Hausdorff distance between spheres" which is joint work with Michael Harrison.(click here to return to top)
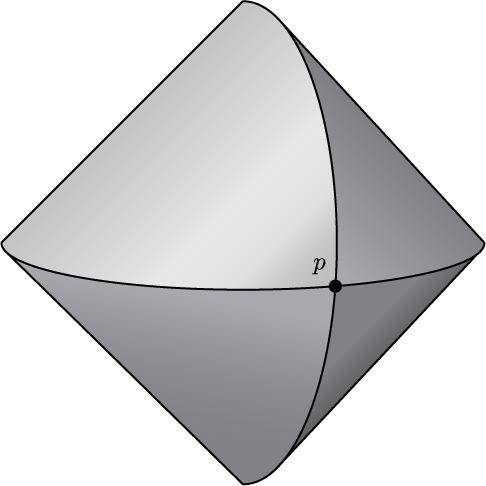A compact convex set in 3-dimensional space, with a boundary point that has the following property: the intersection of the set with any small sphere centered at the point is not geodesically convex. This makes it difficult to generalize a certain 2-dimensional argument. This appears as Figure 6 in "Planar convex codes are decidable" which is joint work with Boris Bukh.(click here to return to top)
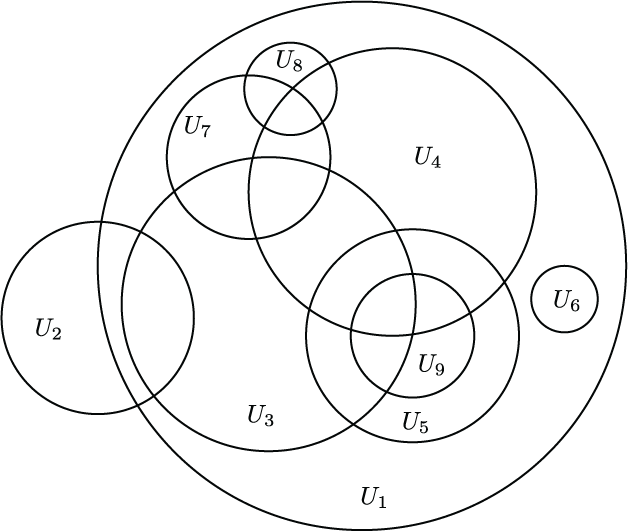A collection of circles in the plane, which can be formed iteratively by adding circles that intersect a collection of previously added circles that share a common point. Such a process can also be described using spheres in higher dimensions, and it always yields an "inducively pierced" code. We give a nice combinatorial classification of such codes. This appears as Figure 3 in "Recognizing and realizing inductively pierced codes" which is joint work with Ryan Curry, Nora Youngs, and Ziyu Zhao.(click here to return to top)
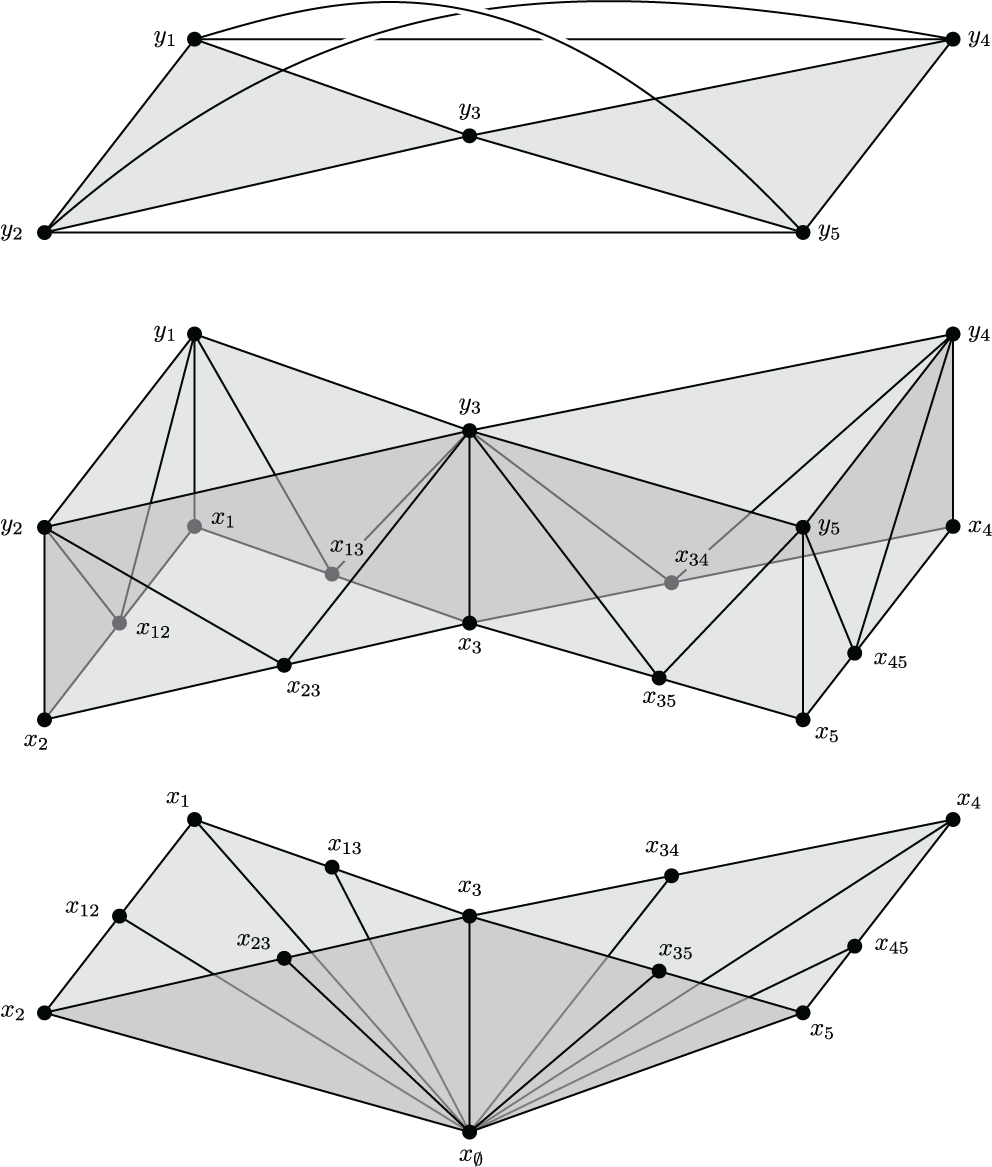The augmented Bergman complex of a (non-matroidal) closure operator, shown in three layers. It has the interesting property that it can be shelled from flags to bases (from the bottom to the top in the figure) but not from bases to flags, due to the bowtie-like subcomplex at the top. This appears as Figure 1 in "Decompositions of augmented Bergman complexes."(click here to return to top)
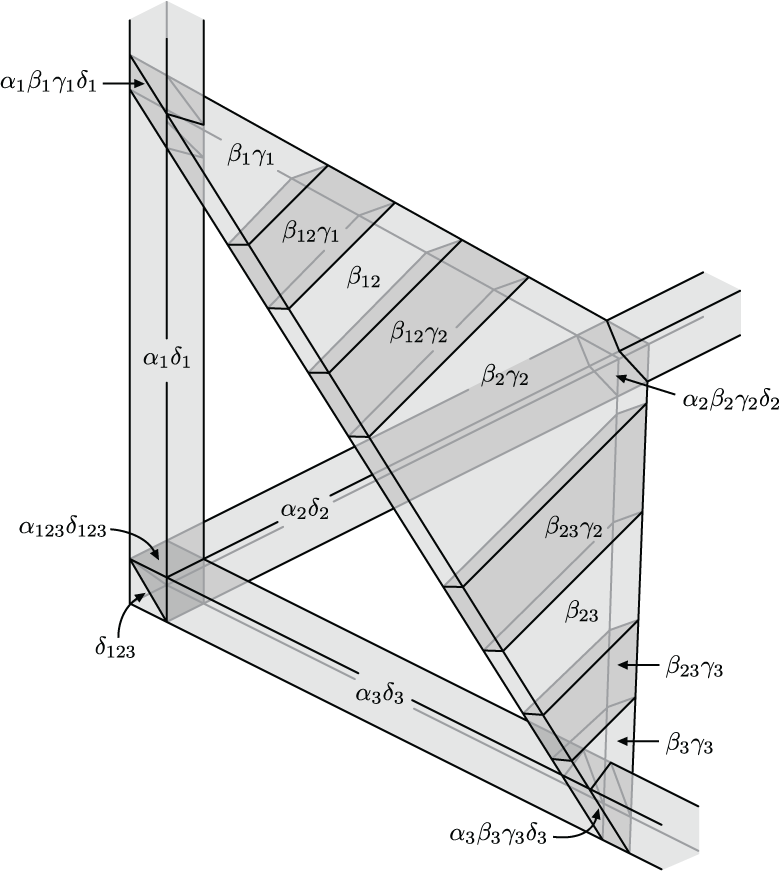
A closed convex realization of a code in 3-dimensional space. Replacing sets by their interiors yeilds the same code. Curiously, one can find a closed convex realization in the plane, but it will never have the property that one can replace sets by their interiors to obtain a realization of the same code. This appears as Figure 6 in "Open, closed, and non-degenerate embedding dimensions of neural codes."
(click here to return to top)
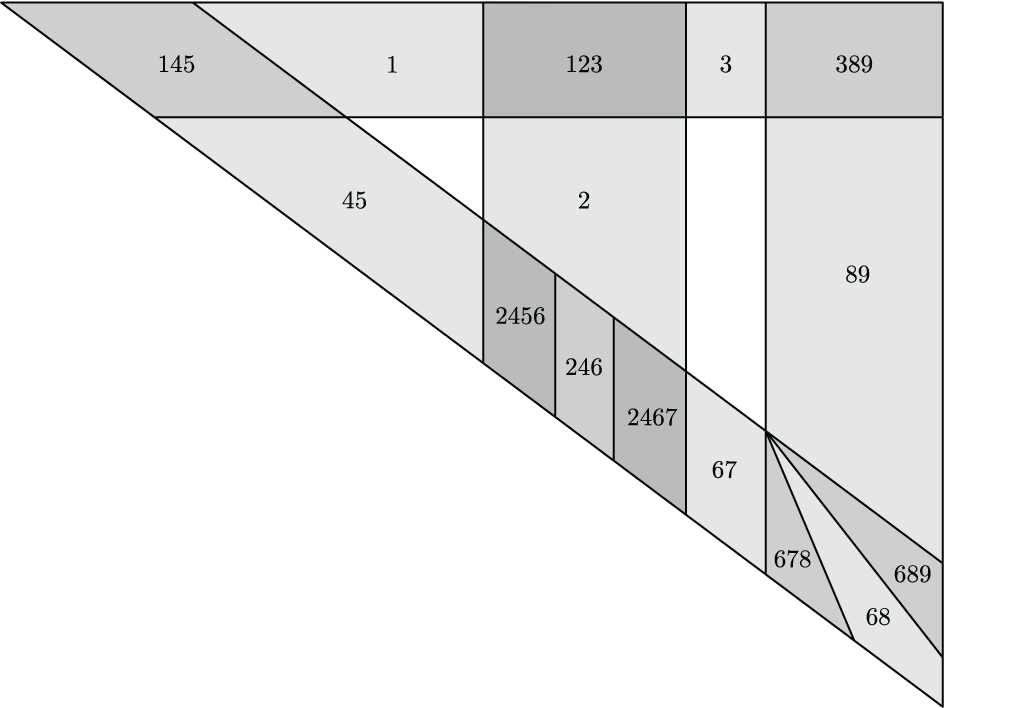
An open convex realization of a code in the plane. Replacing sets by their closures does not yield a realization of the same code, since this will cause the disjoint sets indexed by 7 and 9 to intersect. In fact, this is true for every open convex realization of this code. Nevertheless, one can find a closed convex planar realization (see below). This appears as Figure 10 in "Open, closed, and non-degenerate embedding dimensions of neural codes."
(click here to return to top)
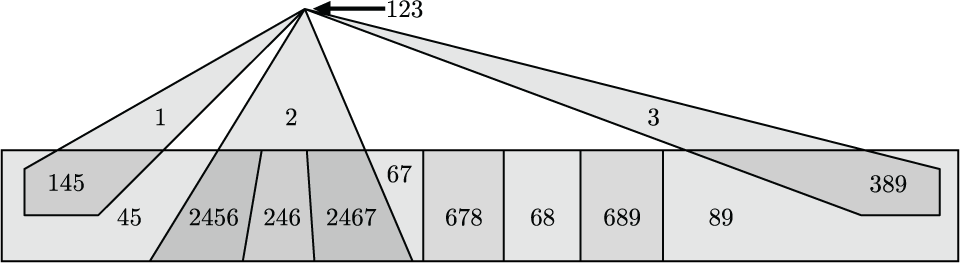
A closed convex realization of the code from above in the plane. Dually to above, no matter how one realizes this code with closed convex sets one cannot use the interiors of those sets to realize the same code. Above, the intersection of the first, second, and third sets will become empty. This appears as Figure 9 in "Open, closed, and non-degenerate embedding dimensions of neural codes."
(click here to return to top)
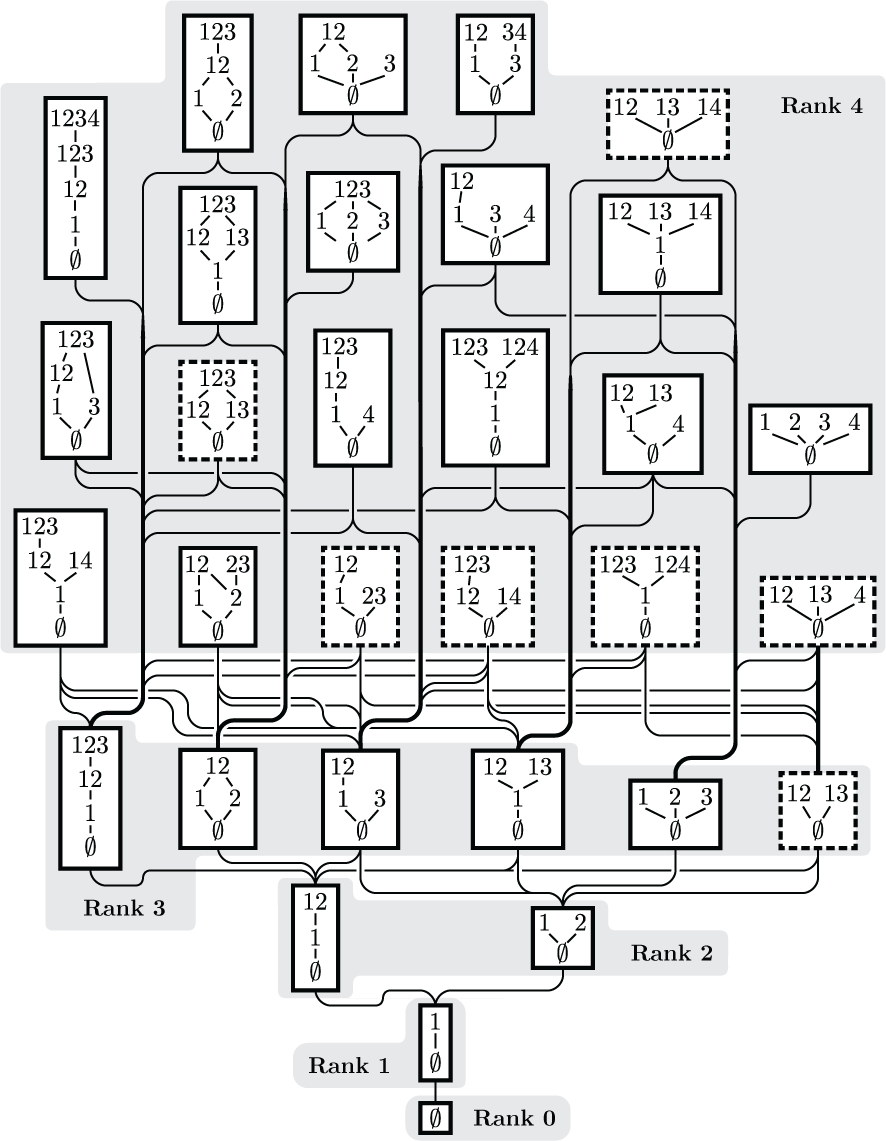
One can partially order all combinatorial codes so that those realizable by convex sets form a downward-closed family. The resulting poset is ranked, and this figure shows its first five ranks. Covering relations are indicated by paths that move down monotonically. Each code is itself displayed as a Hasse diagram, and dashed borders indicate codes that are not intersection complete. This appears as Figure 4.4 in "Morphisms, minors, and minimal obstructions to convexity of neural codes."
(click here to return to top)
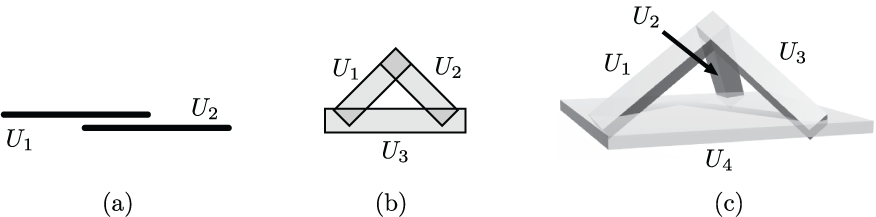
Open convex realizations of the first three "sunflower codes" in dimensions one, two, and three. These realizations are minimal in dimension. This first appeared in "Embedding dimension phenomena in intersection complete codes," and this version appears as Figure 5.9 in "Morphisms, minors, and minimal obstructions to convexity of neural codes."
(click here to return to top)
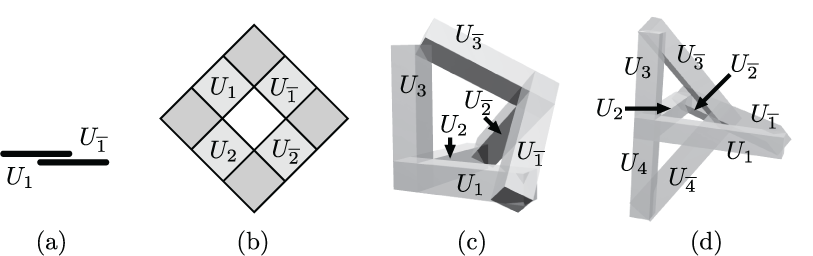
Open convex realizations of the first four "tangled sunflower codes" in dimensions one, two, three, and three. These realizations are minimal in dimension. This first appeared in "Embedding dimension phenomena in intersection complete codes," and this version appears as Figure 5.19 in "Morphisms, minors, and minimal obstructions to convexity of neural codes."
(click here to return to top)
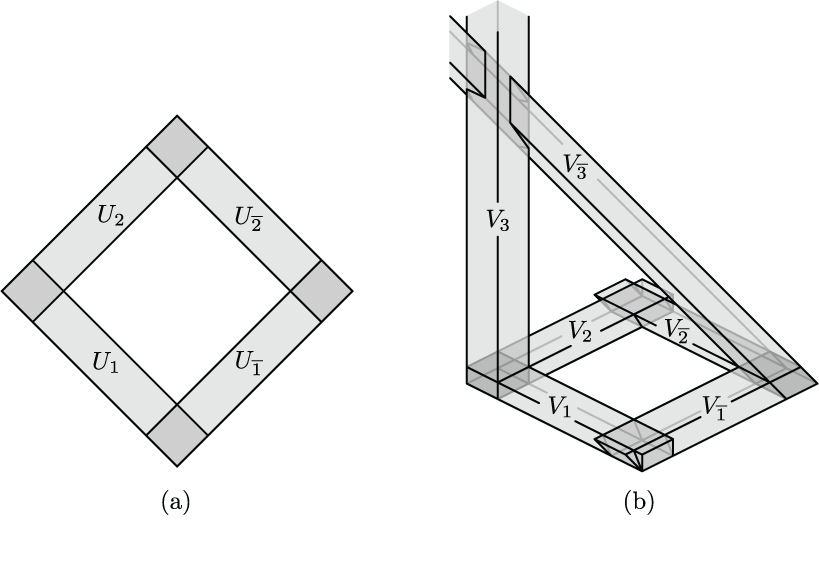
A construction which starts from a d-dimensional realization of the n-th tangled sunflower code and yields a (d+1)-dimensional realization of the (n+1)-st tangled sunflower code. A version of this first appeared in "Embedding dimension phenomena in intersection complete codes," and this version appears as Figure 5.20 in "Morphisms, minors, and minimal obstructions to convexity of neural codes."
(click here to return to top)
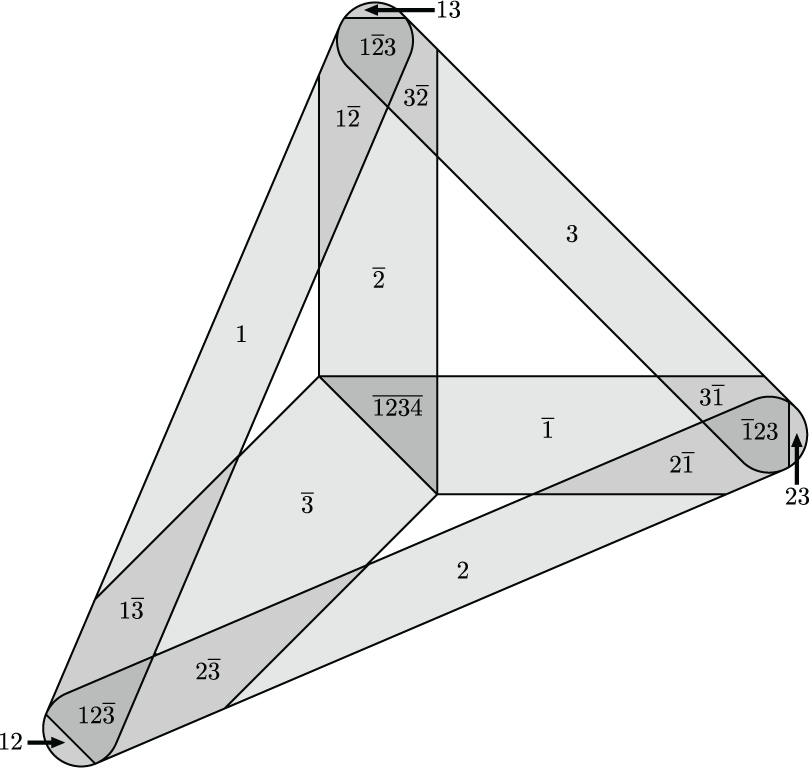
A convex open realization of a code in the plane. Interestingly, if we add the non-maximal codeword 4, the resulting code can only be realized in 3-dimensional space. It turns out there is an analogous code for every dimension, where adding a new non-maximal codeword causes the minimal realization dimension to increase by exactly one. A color version of this appeared in "Order-forcing in neural codes" which is joint work with Caitlin Lienkaemper and Nora Youngs, and this version appears as Figure 5.11 in "Morphisms, minors, and minimal obstructions to convexity of neural codes."
(click here to return to top)
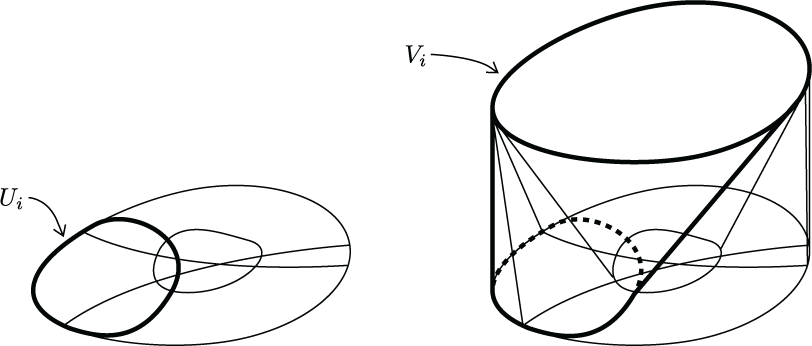
A construction used to prove that a certain family of simplicial complexes, called "convex union representable" complexes, have Alexander duals that are collapsible. The proof uses the fact that sweeping a hyperplane across a d-representation of such a complex induces a sequence of collapses in the complex. This appears in Section 6 of "Convex union representability and convex codes" which is joint work with Isabella Novik.
(click here to return to top)
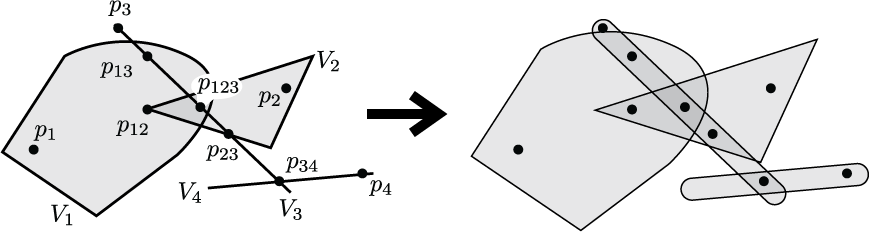
An illustration of the fact that compact convex realizations of codes that are simplicial complexes can be converted to open convex realizations by taking the Minkowski sum of the sets with a small open ball. This appears in the introduction of "Embedding dimension phenomena in intersection complete codes."
(click here to return to top)
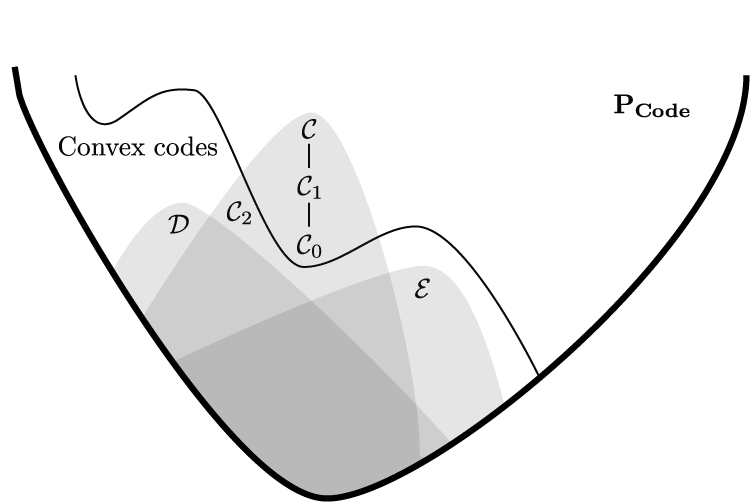
One may partially order all combinatorial codes so that those realizable by collections of convex sets form a downward-closed family. It is then natural to ask which codes are "minimally non-convex" in the sense that they are not realizable, but all codes below them are. This figure shows the process of starting from a known non-convex code, and then computing a minimally non-convex code below it. It turns out there is exactly one such minimally non-convex code, and it lies two covering relations below the starting code. This appears in Section 5 of "Morphisms of neural codes."
(click here to return to top)