Research
My research lies in the fields of nonlinear partial differential equations
and applied analysis. The main focus of my research is on energy-driven
systems --- broadly defined as the systems that dissipate an associated
free energy.
Geometry of gradient flows
Many systems can be
characterized as the steepest descent of the free energy with respect to an
appropriate metric. The metric that determines the dynamics is set by the
mechanism by which the energy is dissipated.
Formally this gives the configuration space a
structure of an (infinite dimensional) Riemannian manifold. This, geometric,
viewpoint of the gradient flows is both physically natural and has proven
very fruitful in obtaining mathematical results.
By studying the geometry of the configuration space itself as well as the
the energy landscape for the energy driving the system one is able to
obtain important properties of the system.
The most studied family of gradient flows for which the configuration
space has a nontrivial geometry are the gradient flows in Wasserstein metric.
They bear that name since the geodesic distance on the configuration space
is the Wasserstein metric --- the optimal transportation metric with
quadratic cost. This is explained in a particularly nice way in the paper
- Felix Otto
, The geometry of dissipative evolution equations: The porous
medium equation, Comm. Partial Differential Equations 26 (2001).
and the book
-
Cedric Villani : Topics in Optimal Transportation, AMS,
Graduate Studies in Mathematics vol. 58 (2003).
I worked on several topics in this area.
In particular on problems related to coarsening behavior which are explained in more detail below.
I also worked on
- (jointly with
Stefano Lisini ,
Jose A. Carrillo ,
and Giuseppe Savar )
Geodesic convexity of energies with respect to a family of metrics where the
local metric depends nonlinearly on the density. For the Wasserstain metric the
dependance is linear. However there are problems in phase segregation and
mathematical biology where the dependance is nonlinear.
The questions of convexity
are important for a number of reasons in particular for
building a rigorous theory of gradient flows in the
given metric.
- (jointly with Jos A. Carrillo ) Determinimg which functionals (energies) are
convex with respect to Wasserstein metric is a delicate question.
We presented the first examples of functionals that involve derivatives, which are
goedesically convex.
- The blowup dynamics of unstable thin-film equations. The gradient flow structure
here plays a role in suggesting the right space and the right coordinates to use when linearizing
the equation.
- (jointly with Robert McCann )
Asymptotic behavior of nonlinear diffusion equations. The convexity properties of the
energy provide plenty of information on the long-time asymptotics of gradient flows.
This theme has been used in many works. We provide a contribution towards
understanding the dynamics of the porous medium equations.
Coarsening
I am particularly interested in nonequilibrium systems --- the ones that stay
far from an equilibrium over long times. Such systems can can have
complex energy landscape with many unstable
stationary points and can display rich dynamical behavior.
An example of such behavior is coarsening. Two examples are shown below.
As a system evolves the length scale characterizing the system grows, while
many other features are preserved. The evolution appears to be statistically
selfsimilar.

|

|
Coarsening in thin liquid films:
Droplets interchange mass through the connecting fluid layer.

|
|
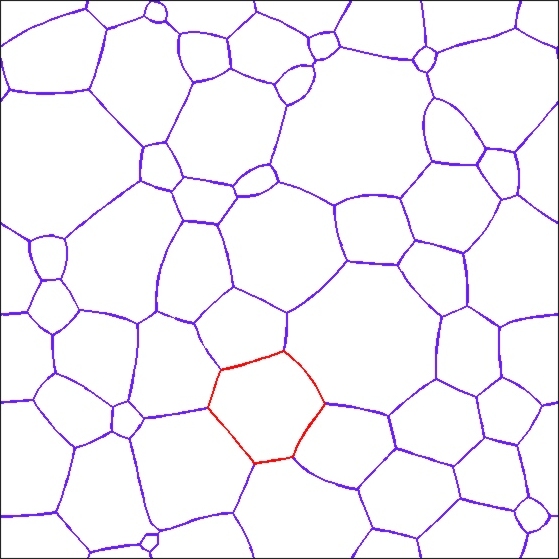
Coarsening in grain-boundary networks:
Interfaces between grains move by mean curvature while preserving the 120
degree angles at triple junctions.
Recent advances, in particular the works of Kohn and Otto,
have made it possible to obtain rigorous information about
dynamical scaling of characteristic length scales
present in complicated evolving patterns.
- In joint projects with
Karl Glasner ,
Felix Otto ,
Tobias Rump,
I worked on coarsening in thin-liquid films.
- With Eva Eggeling and Shlomo Ta'asan , I am working on coarsening in grain-boundary networks.
- With Selim Esedoglu ,
I worked on coarsening in discretizations of ill-posed diffusion equations.
- I worked on coarsening in nonlocal interfacial systems related to phase
segregation
and models of biological aggregation.
Biological aggregation
One of important goals in the area is to understand how simple decisions of individuals
lead to complex collective behavior.
- With Andrea Bertozzi ,
I have been studying a simple model (by Topaz, Bertozzi, and Lewis)
of aggregation
in which individuals exhibit long-range attraction, but have a short-range
mechanism to avoid overcrowding. We found a relationship between these models and
nonlocal interfacial models in phase segregation that explains why the
aggregates (such as herds) form, why they have only small variation in density and show that there are
surface-tension type effects at their boundaries that stabilize them.
- With Jos A. Carrillo ,
Marco Di Francesco ,
Alessio Figalli , and
Thomas Laurent , I am studying a model
in which only attraction is present. In this case collapse of the system to a
single point (delta-mass) is possible.
Bioinformatics
With Gustavo Rohde I recently began investigation of application of
optimal-transportation type metrics in understanding large image data sets.





