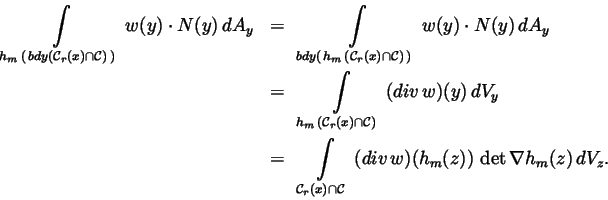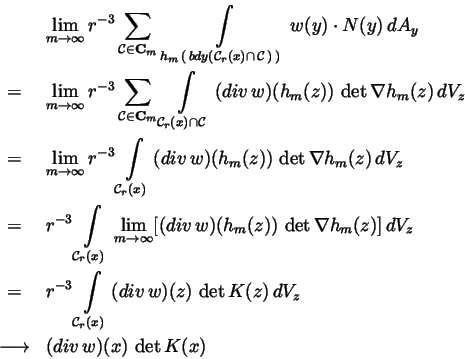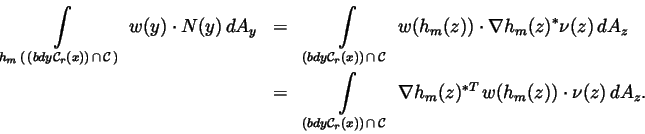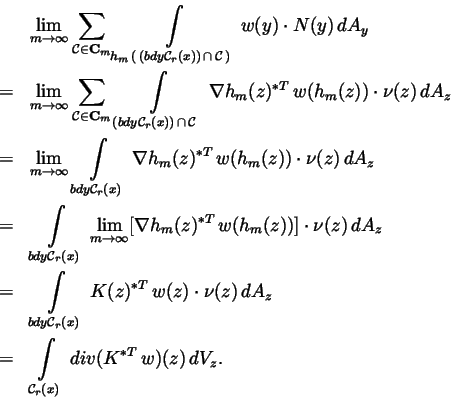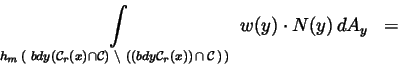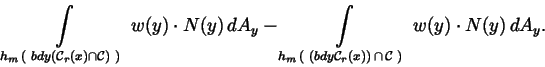Next: Examples of refinements of
Up: Refinements of Balance Laws
Previous: Identification relations
To derive (1.3), we let a positive number r, a positive integer <tex2htmlcommentmark>
m, and cube
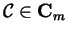 be given, and we use the
relation
be given, and we use the
relation
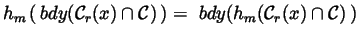 ,
the Divergence Theorem, and the
Change of Variables Formula for volume integrals to write
,
the Divergence Theorem, and the
Change of Variables Formula for volume integrals to write
Summing over all cubes
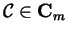 ,
dividing by r3, and
letting
,
dividing by r3, and
letting
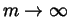 yields
yields
as
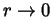 ,
and this establishes the identification relation
(1.3) for
,
and this establishes the identification relation
(1.3) for
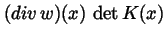 as the volume density of the
total flux of w.
as the volume density of the
total flux of w.
To derive the second identification relation (1.4), we first use
the Change of Variables Formula for surface integrals to write
Summing over
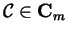 ,
letting
,
letting
 and applying the Divergence Theorem, we conclude that
and applying the Divergence Theorem, we conclude that
The identification relation (1.4) for the volume density of the
flux of w without disarrangements follows upon division of the last
relation by r3 and letting
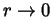 .
.
The last identification relation (1.5) follows immediately from the
first two identification relations, the decomposition of fluxes (1.2
), and the relation:




Next: Examples of refinements of
Up: Refinements of Balance Laws
Previous: Identification relations
Nancy J Watson
1999-09-30
![]() be given, and we use the
relation
be given, and we use the
relation
![]() ,
the Divergence Theorem, and the
Change of Variables Formula for volume integrals to write
,
the Divergence Theorem, and the
Change of Variables Formula for volume integrals to write