



Next: Structured motions
Up: Structured Motions
Previous: Classical motions
Let a subset
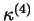 of
of
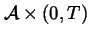 and
and
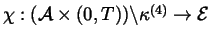 be
given. We call the pair
be
given. We call the pair
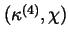 a simple motion of
the piecewise fit region
a simple motion of
the piecewise fit region
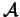 during the time interval (0,T) if
the pair
during the time interval (0,T) if
the pair
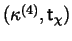 ,
with
,
with
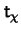 the
trajectory mapping defined in (6.6), is a ``space-time '' simple
deformation, i.e., if
the
trajectory mapping defined in (6.6), is a ``space-time '' simple
deformation, i.e., if
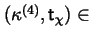 Sid
Sid
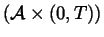 .
.
Example (``blinking motion''): Let
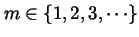 ,
,
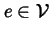 ,
,
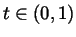 ,
and let
,
and let
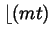 denote
the greatest integer
denote
the greatest integer less than or equal to mt. We define
less than or equal to mt. We define
In this simple motion, the points of the region
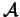 do not move
during the time interval
do not move
during the time interval
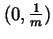 ,
but they suddenly all move at time
,
but they suddenly all move at time
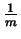 to gain a displacement
to gain a displacement 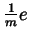 .
The points again remain static
during the interval
.
The points again remain static
during the interval
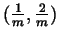 and suddenly displace at time
and suddenly displace at time
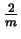 ,
again by amount
,
again by amount 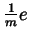 ,
and so on. Thus, if one happened to
blink at each of the times
,
and so on. Thus, if one happened to
blink at each of the times
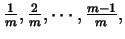 one
would not observe any motion. Nevertheless, at the end of the time interval <tex2htmlcommentmark>
(0,1), the region would have displaced by an amount
one
would not observe any motion. Nevertheless, at the end of the time interval <tex2htmlcommentmark>
(0,1), the region would have displaced by an amount
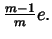 Note
that we have
Note
that we have
for all
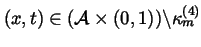 ;
this
relation reflects the fact that in this example movement only occurs at a
finite set of times and distances between points in the body never change.
;
this
relation reflects the fact that in this example movement only occurs at a
finite set of times and distances between points in the body never change.
We write Sim
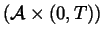 for the collection of
simple motions
for the collection of
simple motions
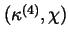 of
of
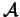 during (0,T).
during (0,T).




Next: Structured motions
Up: Structured Motions
Previous: Classical motions
Nancy J Watson
1999-09-30
![]() of
of
![]() and
and
![]() be
given. We call the pair
be
given. We call the pair
![]() a simple motion of
the piecewise fit region
a simple motion of
the piecewise fit region
![]() during the time interval (0,T) if
the pair
during the time interval (0,T) if
the pair
![]() ,
with
,
with
![]() the
trajectory mapping defined in (6.6), is a ``space-time '' simple
deformation, i.e., if
the
trajectory mapping defined in (6.6), is a ``space-time '' simple
deformation, i.e., if
![]() Sid
Sid
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
and let
,
and let
![]() denote
the greatest integer
denote
the greatest integer![]() less than or equal to mt. We define
less than or equal to mt. We define
![\begin{displaymath}\nabla ^{(4)}\mathsf{t}_{\chi _m}(x,t)=\left[
\begin{array}{cc}
I & 0 \\
0 & 1
\end{array}\right] =:I^{(4)}
\end{displaymath}](img634.gif)
![]() for the collection of
simple motions
for the collection of
simple motions
![]() of
of
![]() during (0,T).
during (0,T).