CARNEGIE MELLON UNIVERSITY
DEPARTMENT OF MATHEMATICAL SCIENCES
21-123 Sequences and Series of Functions
Harmonic Series and Alternating Harmonic Series
Dr. Timothy Flaherty

We shall show that the alternating harmonic series, $\sum_{n=1}^{\infty} \frac{(-1)^{n-1} } {n}$ converges to $\ln 2$. Also, almost immediately, we will deduce that the harmonic series $\sum_{n=1}^{\infty} \frac{1} {n}$ diverges to $\infty$. (In the text, the harmonic series is shown to diverge directly, by the argument in section 11.2 (see example 7). We may also obtain this result from the integral test. Then, after a discussion on alternating series, the alternating harmonic series is shown to converge (see example 1, section 11.5). The actual sum of the alternating harmonic series is only determined through exercise 38, section 11.3, and exercise 36, section 11.5.)

We'll need to consider partial sums of both the harmonic and alternating harmonic series, so set $s_n =\sum_{k=1}^n \frac{ (-1)^{k-1} }{k}$, and $h_n=\sum_{k=1}^{n} \frac{1} {k}$. Then

$$\begin{eqnarray*} h_{2n} & = & 1 + \frac{1}{2} +\frac{1}{3} +\frac{1}{4} + \ldot... ...ac{1}{3} - \frac{1}{4} + \ldots + \frac{1}{2n-1} - \frac{1}{2n} \end{eqnarray*}$$

Subtract these lines to get

$$\begin{eqnarray*} h_{2n}-s_{2n} & = & 2 \left( \frac{1}{2} +\frac{1}{4} + \ldots... ... \frac{1}{2} + \frac{1}{3} + \ldots \frac{1}{n} \\ & = & h_n. \end{eqnarray*}$$

Thus, $s_{2n}=h_{2n}-h_n$. As all $n$ terms in $h_n$ now cancel in this difference, we obtain

$$\begin{eqnarray*} s_{2n } & = & \sum_{k=n+1}^{2n} \frac{1}{k} \\ & = & \sum_{i... ...i} \\ & = & \sum_{i=1}^{n} \frac{1}{n}\frac{1}{1+\frac{i}{n} } \end{eqnarray*}$$

This last expression is the Riemann sum for $f(x)=\frac{1}{x}$ on the interval $[1,2]$ using right-hand endpoints. Thus,

$$\begin{eqnarray*} \lim_{n \rightarrow \infty} s_{2n} & = & \lim_{n \rightarrow \... ..._1^2 \frac{1}{x} \ dx \\ & = & \ln 2 - \ln 1 \\ & = & \ln 2. \end{eqnarray*}$$

Now since $s_{2n+1}=s_{2n}+\frac{1}{2n+1}$, and the last term has limit 0, we obtain that $\lim s_{2n+1}=\lim s_{2n} = \ln 2$. Consequently, $\lim s_n = \ln 2$.

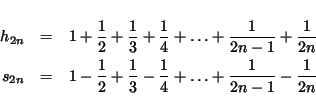
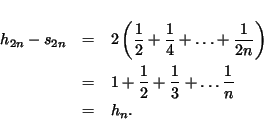
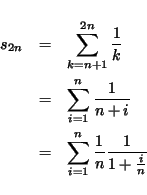
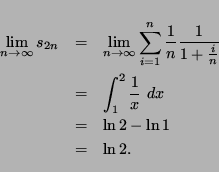
Finally, suppose the harmonic series converges, say $\lim h_n = \gamma$. Then, from $s_{2n}=h_{2n}-h_n$, we would conclude that $\lim s_{2n} = \gamma - \gamma =0$, a contradiction, since $\lim s_{2n}=\ln 2$. Thus, the harmonic series, with increasing partial sums, must diverge to $\infty$.