Packing cubes in a torus

There is a simple packing of 2^d cubes.
Can we ever pack more?
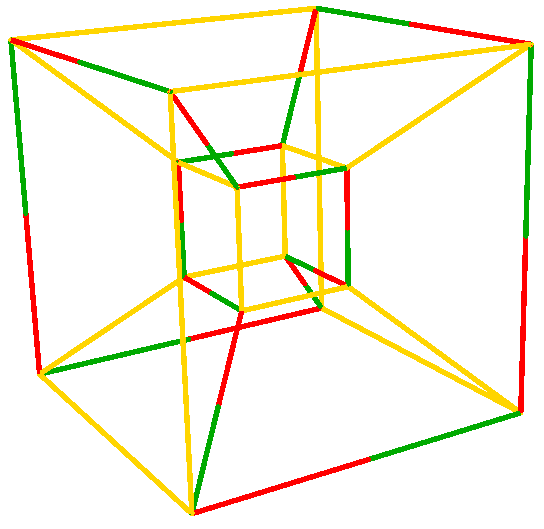
The image above is a depiction of a packing of 17 cubes of side length 3 in the 4-dimensional torus of side length 7. This image and the following explanation of how it depicts a packing are due to Misha Lavrov. This packing problem is related to the problem of determining the Shannon capacity of the complement of the odd cycle C_7. The packing discussed here was first introduced in the paper linked at the bottom of the page.
We pack 17 4-dimensional cubes of side length 3 into a 4-dimensional torus of side length 7 in steps. We begin with a single `central' cube. Then we place 16 additional cubes at the 16 corners of the central cube. Of course, these cubes overlap. To get a proper packing we move each of these 16 cubes (the central cube remains fixed). We move each cube toward the central cube a distance of length 0,1 or 2 in each of the 4 coordinate directions. The picture above shows how far each cube is moved in each direction. Each of the vertices in the 4 dimensional hypercube above corresponds to one of the 16 non-central cubes in our packing. The colors on the half-edges incident with a given vertex show how far the corresponding cubes is moved toward the center cube in each of the directions. A red half-edge corresponds to moving the cube 0 units in the given direction, a yellow half-edge corresponds to moving the cube 1 unit and a green half-edge corresponds to moving the cube 2 units.
To see that this is a propoer packing we have to check that every pair of cubes in the resulting configuration do not overlap. First, we cannot move any of the cubes onto the central cube. Since we move each cube zero units in some direction, we have this property. For every pair of cubes that we actually move, there must be some direction in which the cubes are on oppositise sides of the central cubes and for which the pair of distances moved is (0,2), (1,1) or (1,2). We see by inspection that the distances have this property.
