ABSTRACT: Consider quasilinear elliptic equations of
![]() -Laplacian type
-Laplacian type
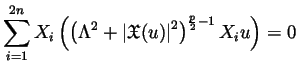 |
(1) |
In the case of the Heisenberg group much less is known without any
additional hypothesis. It was shown by Capogna that the boundedness
of the horizontal gradient
![]() implies the smoothness of
the solution
implies the smoothness of
the solution ![]() . In this talk we will show that when
. In this talk we will show that when ![]() is an
interval
is an
interval
![]() the horizontal gradient
the horizontal gradient
![]() is
indeed locally bounded. Our proof is based on using a type of
unbalanced Moser iteration. We obtain the values
is
indeed locally bounded. Our proof is based on using a type of
unbalanced Moser iteration. We obtain the values
![]() and
and
![]() .
.
This is joint work with Giuseppe Mingione from the University of Parma.