Haim Brezis
Paris VI and Rutgers
New types of Sobolev-Nirenberg imbeddings, isoperimetric
inequalities and elliptic estimates in 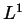
We present new estimates obtained jointly with J. Bourgain, and
partially with P. Mironescu. Each one has a different flavour, but,
in fact, they are closely related.
The first one asserts that
where
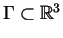 is a closed rectifiable curve,
is a closed rectifiable curve,
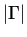 denotes the length of
denotes the length of 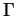 ,
, 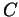 is a universal constant
and
is a universal constant
and
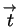 is the tangent to
is the tangent to 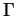 .
.
The second estimate concerns the classical system, in 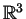 ,
,
Our new estimate asserts that
A third new estimate concerns the system
where 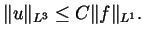 is a divergence-free vector-field. Our new estimate
asserts that
is a divergence-free vector-field. Our new estimate
asserts that
Such inequality is unusual because it is well-known that standard
elliptic estimates fail in 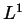 .
.
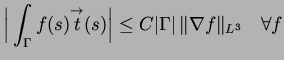
![]() ,
,