Black Box Methods are
the simplest approach to solve constrained optimization problems
and
consist of calculating the
gradient in the following way. Let ![]() be the change in
the cost functional as a result of a change
be the change in
the cost functional as a result of a change ![]() in the design
variables. The following relation holds
in the design
variables. The following relation holds
| (27) |
The
calculation of ![]() is done in this approach
using finite differences. That is,
for each of the design parameters
is done in this approach
using finite differences. That is,
for each of the design parameters ![]() in the representation of
in the representation of ![]() as
as
![]() , where
, where ![]() are a set of vectors
spanning the design space,
one perform the following process
are a set of vectors
spanning the design space,
one perform the following process
ALGORITHM: Black-Box Gradient Calculation
Once the above process is completed for ![]() ,
one combines the result into
,
one combines the result into
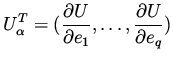 |
(28) |
| (29) |
Since in practical problems the dimension of ![]() may be
thousands to millions, the feasibility of calculating gradients using this
approach is
limited to cases where the number of design variables is very small.
may be
thousands to millions, the feasibility of calculating gradients using this
approach is
limited to cases where the number of design variables is very small.
The Adjoint Method is
an efficient way for calculating gradients for constrained
optimization problems even for very large dimensional design space.
The idea is to use the expression for the gradient as appears in
(18). Thus, one introduces into the solution process
an extra unknown, ![]() , which satisfies the adjoint equation (13).
, which satisfies the adjoint equation (13).
A minimization algorithm is then a repeated application of the following three steps.
ALGORITHM: Adjoint Method