Congestion on Multilane Highways
Introduction
All computations in this section were run with the following equilibrium relations:
 |
(1) |
These transform to
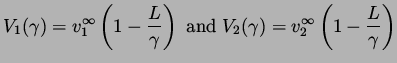 |
(2) |
where
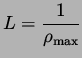 . The specific parameter used were
. The specific parameter used were
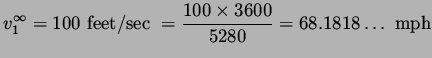 |
(3) |
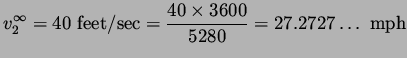 |
(4) |
and
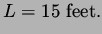 |
(5) |
The latter number corresponds to a maximum car density of
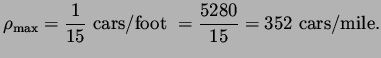 |
(6) |
We used the constant switch curve introduced by Sopasakis [1]:
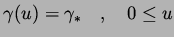 |
(7) |
with
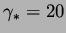 feet. For initial data we chose 3 sets
of data:
feet. For initial data we chose 3 sets
of data:
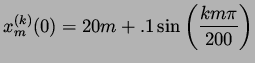 |
(8) |
for
 and
and  , and 3. The observation that
, and 3. The observation that
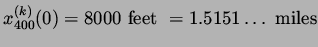 |
(9) |
and
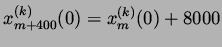 |
(10) |
implies we may interpret the data as initial data for a ring-road with 400 cars which is of length 1.5151... miles. We chose constant initial velocities
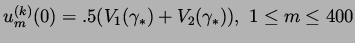 |
(11) |
or
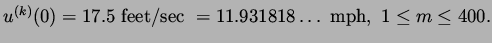 |
(12) |
These data guarantee points on both sides of the switch curve. Simulations were run with relaxation times
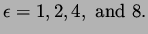 |
(13) |
A word is inorder about the simulations which follow. The first two frames in each figure are self-explanatory. In the third frame of each figure we plot the curve
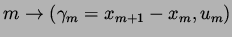 . This curve is shown in black. The blue curves are the equilibrium curves
. This curve is shown in black. The blue curves are the equilibrium curves
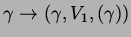 and
and
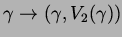 and the red curve is the image of
and the red curve is the image of
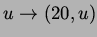 . The red dot - o - is the image of
. The red dot - o - is the image of
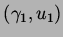 . The discontinuities in the profiles propagate at the speed
. The discontinuities in the profiles propagate at the speed
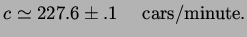 |
(3.14) |
Simulation
Downloads
Lagrangian Representation source code
Eulerian Representation source code
Paper (ps)
Paper (pdf)
Pei-Jen Lin
2001-08-22
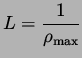 . The specific parameter used were
. The specific parameter used were