Solutions of Neumann problems in domains with cracks and applications to fracture mechanics
Gianni Dal Maso
ABSTRACT: The first part of the course deals with the study of solutions of
the Laplace equation in
,
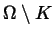where
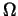is
a two dimensional smooth domain and K is a connected compact subset
of .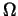
The solutions are required to satisfy a homogeneous
Neumann boundary condition on K and a nonhomogeneous Dirichlet
condition on (part of
.
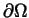The main result is the
continuous dependence of the solution on K, with respect to the
Hausdorff metric. Classical examples show that the result is no
longer true without the hypothesis that K is connected.
The second part of the course uses this stability result
to give a rigorous mathematical formulation of a variational quasistatic
model for the slow growth of a brittle fracture, recently introduced
by Francfort and Marigo. Starting from a discrete time formulation,
a more satisfactory continuous time formulation is
obtained, with full justification of the limit argument. Griffith's
criterion for fracture growth is stated and proved within this model.
Gianni Dal Maso
S.I.S.S.A.
Trieste, Italy
email: Dalmaso@sissa.it
