Johann
for verifying mathematics with combinators

Johann is a toolset for statistically reasoning about computation. At the core of the Johann system is a dynamic database of assumptions and consequences of a theory of computation. The database finitely approximates the semantic space of computations, and provides a language-independent view of computation. Using the database, Johann can answer easy questions about computation and guess answers to difficult questions (and even quantify how sure he is).
The particular model of computation used is inadvertantly-typed concurrent combinatory algebra, i.e., closed-term lambda-calculus with join. The particular theory of computation used is the Hilbert-Post complete theory concurrent-H-star of terms and Scott's information-ordering relation.
For details, see the Documentation Page or Fritz's relevant talks
The maps provided here require an OpenGL visualizer jmapper.
You can download a binary for Mac or Windows or source code for linux/unix.
| Platform | Downloads |
| Mac/Intel | jmapper_mactel.bz2 |
| Mac/PowerPC | jmapper_macppc.bz2 |
| Windows | mapper_win.zip |
| Source Code | mapper.tbz2 |
| Tips on using the jmapper viewer: | |
| up arrow | - zoom in and out |
| + / - keys | - change node size |
| ESCAPE | - exit viewer |
| SPACE | - clear all labels and parse trees |
| s or S | - label simplest terms |
| 1 / 2 / 3 | - select label font size |
| p or P | - toggle label style: combinator or lambda-calculus |
| a or A | - show all parse trees |
| c or C | - toggle hiding of irrelevant nodes |
| right click | - show node's parse tree, hide irrelevant node |
| middle click | - toggle node label |
| left click | - toggle between: parse one step down / parse one step up / don't parse |
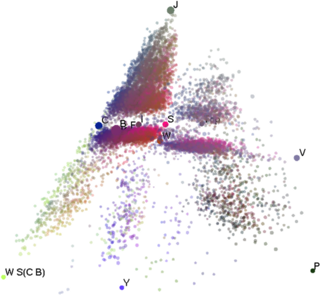
| Sequential Combinatory Algebra - small | ||
| file | untyped.map.bz2 | 
|
| file size | 5.7MB (22MB uncompressed) | |
| programs | 4,803 | |
| equations | 1,666,701 | |
| basis | B, C, S, K, W, C I, 0, 1, 2, S B, B', S', S I, Y, W I | |
| This map took about 1 day to build. | ||
| Sequential Combinatory Algebra - medium | ||
| file | untyped3.map.bz2 | 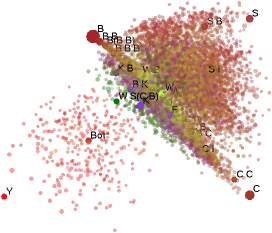
|
| file size | 19MB (74MB uncompressed) | |
| programs | 8,443 | |
| equations | 5,679,089 | |
| basis | B, C, S, K, W, C I, 0, 1, 2, S B, B', S', S I, Y, W I | |
| This map took about 4 days to build. | ||
| Concurrent Combinatory Algebra - large | ||
| file | typed.map.bz2 | 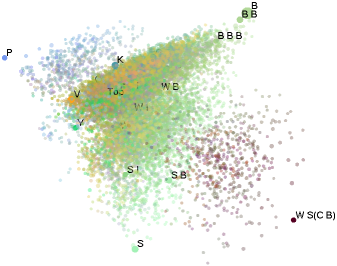
|
| file size | 30MB (125MB uncompressed) | |
| programs | 12,008 | |
| equations | 8,904,419 | |
| basis | B, C, J, S, K, W, C I, V, 0, 1, 2, S B, B', S', S I, Y, W I, P | |
| This map took about 4 weeks to build. | ||