How to read Extended Dynkin Diagrams,

The symbols in describing the (Cayley graphs of) Coxeter groups in the catalog are Dynkin diagrams. Each Coxeter group on n generators r₁,...,r_n can be completely specified by the matrix of orders |r_ir_j| of products r_ir_j. The collection of these numbers defines an n-by-n matrix of natural numbers, called the Coxeter matrix of the group. Since every generator of a Coxeter group is a reflection, the diagonal entries are all 1's. Since the order r_ir_j is equal to the order of r_jr_i, the matrix is symmetric. Finally, each off-diagonal entry is, without loss of generality, at least 2; otherwise the corresponding generators are identical, and n-1 generators would have sufficed.

Dynkin diagrams are a convenient way of representing Coxeter matrices, and are drawn as follows:

draw a circle for each generator r_i.
for each pair of generators r_i,r_j, draw |r_i,r_j|-2 lines between the corresponding circles. (If there are too many lines to draw, simply draw one line labelled by the order |r_i,r_j|.)

The diagrams have some nice properties

If the dynkin diagram of a group consists of k connected components D₁,...,D_k, then the Coxeter group is the direct product of the Coxeter groups defined by each component D_i, as in the 6x8 torus "".
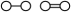In particular, lone circles represent factors of the two-element group Z/2, as in "".

Extended Dynkin Diagrams.

(Note: this notation is not standard)
The polytopes in the catalog are all quotients of the Cayley graph of a Coxeter group (by the vertex symmetry subgroup). For example,

The "free" polytopes in the Coxeter group section are quotients WRT the trivial group, e.g. "".
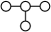The vertices of regular polygons, polyhedra, and polychora are cosets of the symmetry group with respect the subgroup generated by all-but-one of the symmetry group generators, e.g. "" for the pentagon, "" for the dodecahderon, and "" for the 120-cell.
The tori/duoprisms are direct products of regular polygons, e.g. "".
The lattice of quotients of H₄ (the symmetry group of the 120-cell) mirrors exactly the lattice of subsets of its set of four generators, each subset generating a vertex symmetry group.
In particular, the polytope whose vertex-symmetry group is the entire polytope symmetry group (""at the top of the H₄ lattice) is the degenerate 1-cell.

Extended Dynkin diagrams are a convenient way of representing polytopes, and are drawn as follows:

find a presentation of the polytope's symmetry group as a Coxeter group.
draw the Dynkin diagram of the symmetry group.
find the vertex symmetry subgroup of the coxeter group, as generated by some subset of generators of the larger group.
draw a dot in the center of each circle which is also a generator of the vertex symmetry group.

Note that "" and "" are considered the same diagram.

Note that the extended Dynkin diagram symbol of a polytope is not always unique, e.g. the 6x8 torus can be variously denoted by "", "", "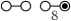", or "".

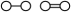Exercise: What are all the extended Dynkin diagrams of the hypercube? (Hint: consult the catalog for some examples.)

Technically the vertex symmetry subgroup induces an equivalence relation on vertices of the (right-)Cayley graph, which induces a graph homomorphism from the Cayley graph down to a "quotient" graph.

Example: The symmetry group of the square is the 8-element dihedral group G = D₈ = "" with Cayley graph the octagon, say generated by a pair of reflections v,e (refer to Figure 1 below). The vertex symmetry group of the square is the two-element reflection group {1,v} about a vertex, generated by v. The (left-)cosets of this set, namely {g{1,v} | g in G} define an equivalence relation on vertices of the Cayley graph. Identifying/merging all Cayley graph vertices in each class results in the quotient graph --the square, i.e., "".

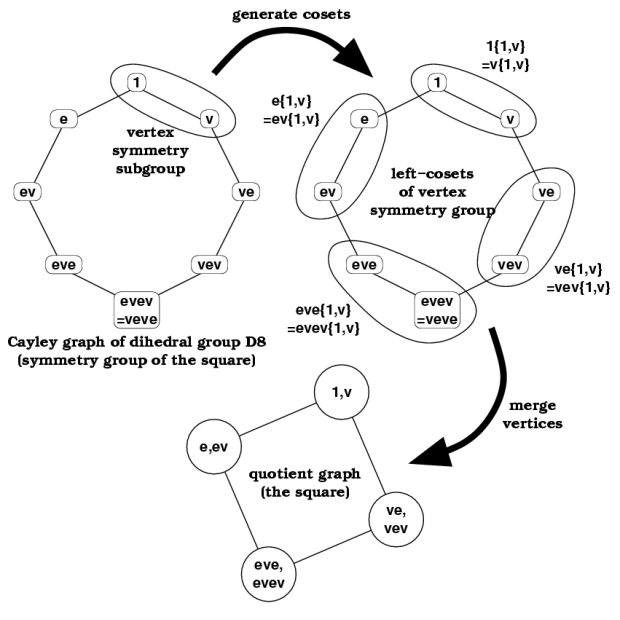
Figure 1. Constructing a quotient graph "

" from the Cayley graph of its symmetry group "

References.

Dynkin diagrams are employed, e.g., in Conway's Atlas of Finte Groups.
Also see Mathworld's explanation.

back to the Catalog of Polytopes