2006 B3
Problem
Let $S$ be a finite set of points in the plane. A linear partition of $S$ is an unordered pair $\{A,B\}$ of subsets of $S$ such that $A\cup B=S$, $A\cap B=\varnothing$, and $A$ and $B$ lie on opposite sides of some straight line disjoint from $S$ ($A$ or $B$ may be empty). Let $L_S$ be the number of linear partitions of $S$. For each positive integer $n$, find the maximum of $L_S$ over all sets $S$ of $n$ points.
Discussion
This problem can be solved by just playing with it, but I was equipped with one slightly suggestive problem that I had solved before:
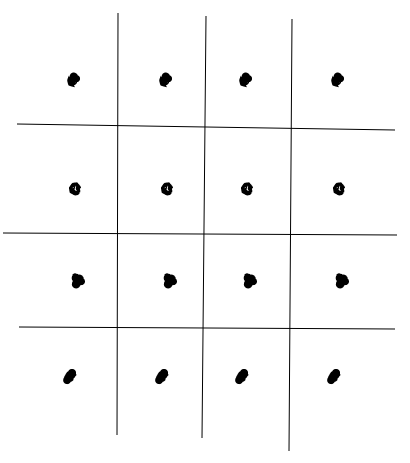
Problem: Consider the set of points $\{(i,j):1\le i\le n\}$. What's the minimum number of lines we need to draw on the plane to divide the plane into regions in such a way that each region has at most one of these points?
Solution: First, we can guess that the solution will be around $2(n-1)$ since we can draw the lines $x=i+\frac12$ for each $1\le i\le n-1$ and $y=i+\frac12$ for each $1\le i\le n-1$, as illustrated:
But the clever way to prove the lower bound in this problem is by considering each of the $4(n-1)$ segments along the perimeter of the figure:
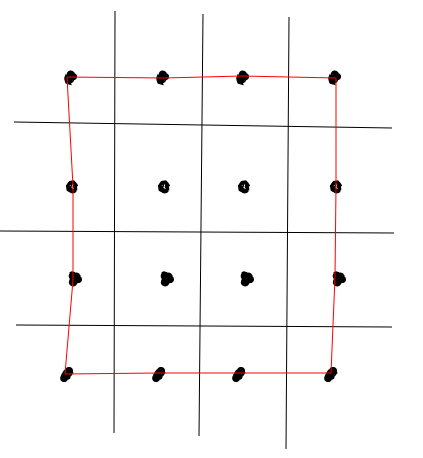
Since each of these segments must have some line going through it, and each line can go through at most $2$ segments, then there must be at least $2(n-1)$ lines.
Now we get back to the problem. The problem I just mentioned is just something to keep in the back of your head. Another thing you should think of is wanting to minimize the number of collinear points in the configuration of points. Upon drawing a regular $n$-gon for small values of $n$ and seeing how good they do, we can guess the pattern that each time we guess that $L_{\text{regular}~n\text{-gon}}=\binom{n}2+1$. But how can we prove such a bound? In fact, if we are bold enough, we can conjecture the following claim: for any set $S$ such that no three points in $S$ are collinear, there are exactly $\binom{n}2+1$ linear partitions.
The following idea is motivated by the fact that $\binom{n}2$ is the number of ways to choose pairs of points from these $n$ points, and the $+1$ corresponds to some trivial linear partition (for example, the partition of $S$ into $\{S,\varnothing\}$). We will try to find a bijection between the number of nontrivial linear partitions and the number of ways to choose two points. For each pair of points $\{X,Y\}$ such that $X,Y\in S$, we are going to draw a line $\ell$ through $X$ and $Y$ and then rotate it sliiiightly clockwise about the midpoint of $X$ and $Y$. How slightly though? Slightly enough so that it doesn't hit any other point in $S$ while we're rotating it. This is always possible because there is a finite number of points and an infinite number of small angles we can rotate it, which means one angle is small enough so that it doesn't hit any other ponit. Therefore, we can call $f(X,Y)$ to be the partition we get by this process. How do we know that $f$ is a bijection? That takes a little more proving.
First we show that $f$ is surjective (except for the trivial case). Given a linear partition of $S=A\sqcup B$ by $\ell$ such that $A,B\neq\varnothing$, we can slide $\ell$ in a parallel fashion until it hits some element of $X\in A$ (in the event that $\ell$ is hitting two elements $X_1,X_2\in A$ at this moment, choose the one that is counterclockwise along the convex hull of $A$. And if you want to be super pedantic, you should also address the case where the convex hull of $A$ only has two points on it, but I'm not going to do that). We will then traverse the convex hull of $A$ via the following process, which should look like a windmill: rotate $\ell$ counterclockwise about $X$ until $\ell$ hits another vertex $X'\in\mathcal{C}(A)$, then use $X'$ as the new pivot until $\ell$ hits yet another vertex in $\mathcal{C}(A)$, and so on. We stop at the first moment that $\ell$ hits an element of $Y\in\mathcal{C}(B)$. Since no three points are collinear in $S$, at this moment $\ell$ is passing through two unique points $X\in A$ and $Y\in B$. From here, it's not extremely hard to prove that $f(X,Y)=\{A,B\}$, it involves just noting something about the convex hull. I will elaborate if requested to do so.
Now to show that $f$ is injective, suppose $\{A,B\}=f(X_1,Y_1)=f(X_2,Y_2)$ for $X_1,X_2\in A$ and $Y_1,Y_2\in B$, where $(X_1,Y_1)\neq(X_2,Y_2)$. Really all you have to do now is just do some casework on how $\{X_1,X_2,Y_1,Y_2\}$ are configured.
Having proven this claim, it's not too hard to finish. We have to prove that $\binom{n}2+1$ is maximal. The idea now is to take a maximal configuration and modify the points just a tiny amount so that it does not decrease the number of linear partitions, but move them enough so that no three points in the resulting set are collinear. At this point the set will have $\binom{n}2+1$ lines, which means that would be the maximum. Now how do we do this? Take a configuration with a maximal number of linear partitions, and let $\{\ell_i\}_{i=1}^m$ be a set representatives from each of the $m$ partitions. For each point $X\in S$, each $\ell_i$ divides the plane into two regions, one of which contains $X$. Thus, let $R(X)$ be the intersection of all such regions. But each $R(X)$ is a convex polygon since it is the intersection of half-planes! Therefore, we can perform the following algorithm: let $S=\{X_1,\dots,X_n\}$, and for $i=3,4,\dots,n$, let $X_i'\in R(X_i)$ be such that $X_i'$ is not collinear with any of $X_1,X_2,X_3',X_4',\dots,X_{i-1}'$. Such a point exists since there are only a finite number of lines it can lie on but an infinite number of places in $R(X_i)$ to choose from. After the algorithm, we will have a new set $S'=\{X_1,X_2,X_3',\dots,X_n'\}$ such that each of the linear partitions of $S$ are also linear partitions of $S'$, but $S'$ has no three collinear points. Therefore, $m\le\binom{n}2+1$. With this, we have solved the problem.