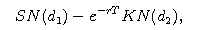
The most important event in the development of computational finance was the publication in 1973 of the Black-Scholes option pricing formula. Developed by Fischer Black and Myron Scholes, with substantial assistance by Robert Merton, this formula tells how to compute the price of an option to buy a share of stock at a future date but at a price agreed upon before that date. While such options are important in their own right, the more important aspect of the work of Black, Merton and Scholes was that it initiated a whole body of work on how to price derivative securities, securities whose price is derived from the price of some other security. (The price of a stock option is "derived" from the price of the underlying stock on which the option is written via the Black-Scholes formula.) Scholes and Merton won the 1997 Nobel Prize in Economics for their work. Fischer Black would no doubt have shared in this prize if he had not died two years earlier.
The Black-Scholes formula says the price of an option to buy a stock at a price K at time T units in the future should be
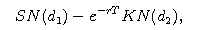
where
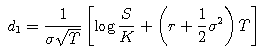
and
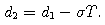
In this formula, N is the standard cumulative normal distribution (the bell-shaped curve), given by
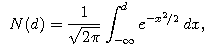
S is the stock price at the time the option is priced, r is the interest rate at which money can be borrowed, and the critical parameter σ is the volatility of the stock, a measure of how risky the stock is. The derivation of the formula requires a good understanding of calculus and probability theory. Its use as a guide for buying and selling options requires one to also understand financial markets. The discovery of the Black-Scholes formula facilitated the growth in options trading. It also sparked the search for similar formulas for more complicated derivative securities, and this has revolutionized the finance industry.
| ⇐ Back | Next ⇒ |