

Take a sheet of graph paper (the bigger the squares, the better). What shapes can you cut out using the squares?
A domino is a shape made from two adjacent squares. These are dominoes:


By modifying the word domino, we can get names for similar shapes that use different numbers of squares. First, we have the lonely monomino, made of just a single square:

If we use three connected squares, we get a tromino (or a triomino). These are the trominoes:






Four connected squares make a tetromino. These are the tetrominoes:










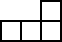








There are names for larger shapes like this, too. Five connected squares make a pentomino, six connected squares make a hexomino, seven connected squares make a heptomino, and so on; these names come from the Greek words for five, six, seven, etc.
In general, a polyomino is any shape formed from connected squares like this. So dominoes, trominoes, and tetrominoes are just different sizes of polyominoes.
Above we listed one monomino, two dominoes, six trominoes, and 19 tetrominoes. However, this is not the only way to think about polyominoes. There are two other common ways to distinguish polyominoes.
Usually we like to think of the two dominoes as the same shape, because we can get one of them from the other by just rotating it 90 degrees. If we follow this convention, there is essentially just one domino, not two:

Likewise, we often consider the two “straight” trominoes to be the same, and the four “bent” trominoes to be the same, because we can get the others by rotations. If we think about things this way, we have essentially just two trominoes, not six:


And we have essentially just seven tetrominoes, not 19:







Notice that the last two pairs of tetrominoes above look very similar, but we cannot rotate one of them to get the other. Instead, we would have to pick up the shape and flip it over, which we are not allowing (yet). So, according to this particular convention, we consider them to be different shapes. (These seven shapes are the familiar Tetris pieces. If you’ve played Tetris, you are familiar with the idea of being able to rotate pieces but not flip them over.)
In the third common way of thinking about polyominoes, we allow rotations and reflections (flipping pieces over). In other words, if one polyomino can be turned into another by rotating it, picking it up and flipping it over, or both, then we consider the two polyominoes to be the same. This brings the number of tetrominoes down to just five:





Let’s call polyominoes “fixed” when we use the first convention, because we imagine that they can be neither rotated nor flipped over. (If we rotate one or flip one over, we consider the resulting polyomino to be different.) Polyominoes are called “one-sided” when we follow the second convention, because they can be rotated but not flipped over; and they are called “free” when we use the third convention, because we are free to rotate them or flip them over however much we like.
Any of these three points of view is valid and interesting. Most polyomino puzzles, however, use free polyominoes, in order to maximize the number of ways the polyominoes can be manipulated.
Here are some questions to think about. Some of them require quite a bit of thought and experimentation. Some of the questions ask for something which is impossible. (For example, it is impossible to make a rectangle using all of the free hexominoes.) If you think it can’t be done, then the question becomes, why? Actually, a few of the questions below are unsolved—no one in the world knows the answer. Perhaps you could be the first one! (If you are interested in knowing about these, let me know and I can give you some specific unsolved problems to play with.)
It will probably be helpful to get some graph paper to draw on. Cutting out polyominoes from graph paper is also helpful, so that you can play with them on a desk to help you visualize how they fit together.
The area of a polynomino is the number of squares it contains: the area of the monomino is 1, the area of a domino is 2, and so on. How many polyominoes are there of a given area?
To answer this question, we need to choose one of the conventions described above so that we can say when two polyominoes are different. Our results so far are summarized in the following table.
| Name | Area | Fixed polyominoes | One-sided polyominoes | Free polyominoes |
|---|---|---|---|---|
| Monomino | 1 | 1 | 1 | 1 |
| Domino | 2 | 2 | 1 | 1 |
| Tromino | 3 | 6 | 2 | 2 |
| Tetromino | 4 | 19 | 7 | 5 |
| Pentomino | 5 | |||
| Hexomino | 6 |
Choose one of these three conventions. List all of the different pentominoes to figure out how many there are. (Be careful that you aren’t listing any shape twice and that you aren’t missing any shapes.) Can you find a pattern in these numbers? If so, make a prediction for how many hexominoes there are, according to the pattern you found. Then list all of the different hexominoes. Was your prediction correct?
For a real challenge, try to list all of the heptominoes (polyominoes with area 7). Be careful—one of the heptominoes has a hole!
We can also think about the perimeter of a polyomino, which is the distance around the outside edge. We consider each of the little squares to have a side length of 1. So, for example, the monomino has a perimeter of 4, and a domino has a perimeter of 6. How many polyominoes are there with a given perimeter?
Again, to answer this question, we first need to choose one of the conventions described above so that we can say when two polyominoes are different. It is easy to see that the smallest possible perimeter is 4, because that is the perimeter of a single square. So, if we make a table like the one above, we can start with 4:
| Perimeter | Number of polyominoes |
|---|---|
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 |
Start classifying the polyominoes by their perimeter and complete the table above. (Don’t forget to specify which convention you’re following.) Can you find any patterns in these numbers?
For a given area, what shape of polyomino gives the largest perimeter? What shape gives the smallest perimeter? If you like to think about things algebraically, let n represent the area of a polyomino. Can you find an algebraic expression in terms of n that gives the largest or smallest perimeter possible for a polyomino with area n?
Which polyominoes can tile the plane?
In other words, if you have a big box filled with a bunch of copies of one particular polyomino, can you fit them together to cover a large floor without any gaps or overlap? For some polyominoes, the answer is yes, but for other polyominoes the answer is no. Can you find some common characteristic shared by those polyominoes that can tile the plane?
Does the answer change if you work with a one-sided polyomino or a fixed polyomino rather than a free polyomino?
Choose one of the three conventions described above, and choose a particular size of polyomino (for example, the tetrominoes). Now suppose you have one copy of each of these polyominoes. Can you fit all of them together to make a rectangle without any gaps or overlap? (A good place to start is to figure out what the total area of such a rectangle would have to be, so that you can come up with a list of possible dimensions for the rectangle.)
What if you have two copies of each polyomino? Three copies?
The five free tetrominoes have a total area of 20. Can you use one copy of each of the free tetrominoes, plus one pentomino, to form a 5 × 5 square?
Can you use one copy of each of the polyominoes of a particular size to form two rectangles with the same dimensions?
Suppose that you have an 8 × 8 checkerboard and a bunch of dominoes (32 of them, to be precise), sized so that the squares that make up the domino are exactly the same size as the squares on the checkerboard. Can you find a way to tile the checkerboard with the dominoes? In other words, can you cover the checkerboard with the dominoes so that all of the squares are covered and no dominoes overlap or hang off the edge of the checkerboard?
Now suppose you remove one of the corner squares of the checkerboard, and then also remove the diagonally opposite corner square. You also throw away one of your dominoes. So you have 62 squares remaining on the checkerboard, and 31 dominoes. Now can you find a way to tile the checkerboard with the dominoes? If not, why not?
Go back to the original 8 × 8 checkerboard. You have a single monomino and a bunch of “bent” trominoes (the L-shaped ones). Choose any square of the checkerboard, and put the monomino there. Can you tile the rest of the checkerboard with the trominoes? Does it matter which square you put the monomino on? What if you use the “straight” trominoes instead?
Plainly it is impossible to tile an 8 × 8 checkerboard with pentominoes, because there are 64 squares on the checkerboard, and 64 is not divisible by 5. But suppose you first cover up four squares with, say, the square tetromino. Can you tile the remaining 60 squares with pentominoes? (What if you make the additional requirement that no pentomino be used more than once?) What if you cover up a different set of four squares (perhaps not adjacent to each other)?
Imagine a long, narrow checkerboard that has many files (columns) but only two ranks (rows). How many ways are there to tile this checkerboard with dominoes? To answer this question, consider small cases first:
| Board size | Number of tilings |
|---|---|
| 2 × 1 | |
| 2 × 2 | |
| 2 × 3 | |
| 2 × 4 | |
| 2 × 5 | |
| 2 × 6 | |
| 2 × 7 | |
| 2 × 8 | |
| 2 × 9 | |
| 2 × 10 |
Can you see any pattern? If you do see a pattern, can you give an explanation for it?
Start with an empty 8 × 8 checkerboard and one copy of each of the pentominoes. Take turns choosing one pentomino and placing it on the board without overlapping a pentomino that has already been placed. The winner is the last person who can play.
Can you devise a strategy for this game? What if a different size board is used? What if different polyominoes are used? What if the object of the game is changed so that the winner is the first person who is unable to play?
Choose one of the free pentominoes. Can you use nine of the other free pentominoes to form a scale model of the shape you chose, three times as wide and three times as high?
Can you do this with other sizes of polyominoes?
We can exclude a particular polyomino from the 8 × 8 checkerboard by placing a number of monominoes (thereby blocking certain squares) in such a way that there is no open place on the board where the polyomino will fit.
Choose one particular polyomino. Can you find a way to exclude this polyomino from the 8 × 8 checkerboard using as few monominoes as possible? What if you want to exclude several (or all) of the polyominoes of a certain size simultaneously? What if you use dominoes (or some other polyomino) instead of monominoes to block squares?
Can you extend the idea of polyominoes into three dimensions by considering arrangements of cubes?
We defined polyominoes above to be groups of squares that are connected along their edges. Can you change this connectivity rule? For example, what if you allow squares that touch diagonally?
The polyominoes described above are based on a square grid. What happens if you use a triangular or hexagonal grid instead? (The hexagonal analog of polyominoes is important in organic chemistry, because they describe the structure of certain molecules called polycyclic aromatic hydrocarbons.) How about a grid like the bricks in a wall, or like a floor tiled with two or three different shapes?
Perhaps you can change the rules by which polyominoes are allowed to fit together. For example, what happens if you color the edges of the squares that make up each polyomino, using two or three colors, and then require that touching polyominoes must match colors along their touching edges?
Can you invent a wordplay puzzle by adding letters to the squares of polyominoes?
The classic book on polyominoes is Solomon W. Golomb’s Polyominoes: Puzzles, Patterns, Problems, and Packings. Golomb “invented” polyominoes in 1953 (or at least he invented the word polyomino and helped to introduce them to a wide audience; puzzles involving these shapes had been published at least as early as 1907).
Our textbook Problem Solving Through Recreational Mathematics by Averbach and Chein also briefly discusses polyominoes. See Sample Problem 8.2 on page 274, the section about polyominoes (and the Soma cube) on pages 281 through 285, and Exercises 8.9 and 8.10 on page 308.
There are many pages on the Internet about polyominoes and polyomino puzzles. A good place to start is the at <http://en.wikipedia.org/wiki/Polyomino>.