Abstract

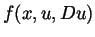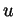The talk is based on my joint work with Jan Maly: ``Approximation in Sobolev spaces of nonlinear expressions involving the gradient". Ark. Math. 40 (2002), 245-274. We investigate a problem of approximation of a large class of nonlinear expressions , including polyconvex functions, that appear in calculus of variations. Here is a mapping from the Sobolev space 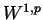. In particular, when 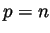, we obtain an approximation by mappings which, from the point of view of applications, are almost as good as Lipschitz mappings. As far as we know, for nonlinear problems that we consider, no natural approximation results were known before. 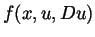The results about the approximation of are consequences of the main result of the paper on a very strong approximation of Sobolev functions by locally weakly monotone functions.

TUESDAY, October 19, 2004
Time: 1:30 P.M.
Location: PPB 300