Monotonicity Properties of Ground States
Patricio Felmer
Universidad de Chile
Centro de Modelamiento Matematico
email: pfelmer@dim.uchile.cl
Abstract: It has been well-known that the scalar field
equation
admits ground state solutions if and only if
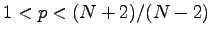 . For each fixed
. For each fixed
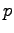 in this range, there corresponds a unique ground state (up to
translation), as well as a unique positive solution to the Dirichlet boundary
value problem
in this range, there corresponds a unique ground state (up to
translation), as well as a unique positive solution to the Dirichlet boundary
value problem
for any finite ball 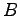 in
in 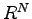 . In this talk we show that the maximum value
of such ground states,
. In this talk we show that the maximum value
of such ground states, 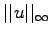 , is an increasing function of
, is an increasing function of 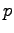 for
all
for
all
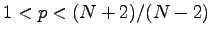 , with
, with
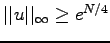 , and
, and
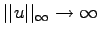 as
as
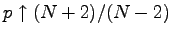 . Consequently, we derive a Liouville type
theorem ensuring that there exists neither a ground state solution to this
equation, nor a positive solution of the Dirichlet problem in any finite ball,
with the maximum value less than
. Consequently, we derive a Liouville type
theorem ensuring that there exists neither a ground state solution to this
equation, nor a positive solution of the Dirichlet problem in any finite ball,
with the maximum value less than 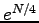 . Our proof relies on some fine
analyses on the first variation of ground states with respect to
. Our proof relies on some fine
analyses on the first variation of ground states with respect to 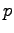 . The
delicacy of this study can be evidenced by the fact that, on any fixed finite
ball, the maximum value of positive solutions to the Dirichlet problem is never a monotone function of
. The
delicacy of this study can be evidenced by the fact that, on any fixed finite
ball, the maximum value of positive solutions to the Dirichlet problem is never a monotone function of 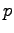 over the whole range
over the whole range
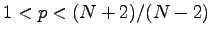 . We will also present some related problems and open
questions.
. We will also present some related problems and open
questions.
The main result is obtained in collaboration with Quaas, Tang and Ye.